Neural network-based prediction of consented organs utilization
Introduction
Organ scarcity is a pressing matter that requires serious attention. According to the US Department of Health and Human Services, a patient is added to the transplant waiting list every 10 minutes (1). As of December 2019, 73,934 people were waiting for a lifesaving organ (2). Although many people are registered on the organ waiting lists, available organs do not meet the need. In 2019, there was a national daily average of 95 transplants, meaning about 19,250 donors supplied at least one lifesaving organ. While it appears to be a considerable number, it does not cover the need (2).
To bridge this significant gap, multiple areas could be improved. The problem could be tackled by increasing the number of people willing to donate an organ after death through sensitizing the communities and groups that usually hold misconceptions about organ donation. Organ Procurement Organizations (OPOs) make immense efforts to reach the communities and convince them to be enrolled to donate after death (3). Another way could be to increase the number of consented organs at the time of death by approaching more families than currently done. This process is carried on by the organ procurement organization staff, who engage with the potential donor family to convince them of donation. Last but not least, increasing the use of the organs recovered would have a tremendous effect on substantially reducing the number of patients on the waiting list (1).
Organ procurement organizations are the main actors in the donation process in the United States. They oversee the process from consent to organ recovery in a complicated, intricate system that involves a large number of unpredictable factors. For this paper, a referral to the OPO from a hospital can result in three outcomes. In the best case, the deceased patient is a registered organ donor, or the family consents to organ donation, and the recovered organ(s) are transplanted. In the worst case, none of the organs are recovered because the family declines organ donation, and the patient had not previously agreed. The third possible outcome is consented but not recovered (CNR), where consent is obtained but no organ is recovered because of an unforeseen medically unsuitable circumstance. These CNR cases require multiple resources in a time-consuming process to obtain consent but do not result in recovered organs. Therefore, there is an opportunity to either convert CNRs into donors or better manage the cases that are more likely to become CNRs. Thus, if the likelihood of the cases proceeding donation can be predicted, resources could be better managed or utilized in cases with a higher probability of resulting in organ recovery and transplant (2).
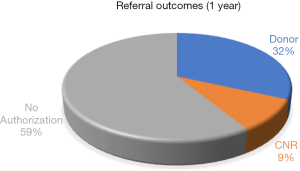
Figure 1 depicts the distribution of the three outcomes for almost two years. Suppose the system could prevent willing donors from becoming CNRs and better anticipate circumstances that result in CNRs. In that case, available resources could be better focused on cases with a greater probability of successful organ recovery and transplant. The process improvements would also spare grieving families anguished discussions about donations when the organs may not be used after all.
The main objective of this paper is to identify the best performing artificial neural network model (backpropagation, resilient propagation, or globally convergent propagation) that can predict the CNR outcome. In addition, identify the key factors that contribute to this outcome and understand why and how they create that effect to better inform the donation process. The clinical significance of predicting CNR cases is to understand the leading factors of this outcome better. Knowing the possible chances of organ recovery of a specific case may affect the donation plan for that specific patient and help maximize the chance of converting it to a donor, thus increasing organ utilization. Furthermore, early identification of such outcomes can allow the medical staff to focus on cases where the probability of organ recovery is higher.
This paper is organized as follows: Section 2 reviews the literature on applications of neural networks in similar research. Section 3 describes the sample data and approach. Section 4 discusses experimental results. Lastly, Section 5 summarizes the findings and provides insight for future research. We present the following article in accordance with the MDAR reporting checklist (available at https://jmai.amegroups.com/article/view/10.21037/jmai-21-9/rc).
Literature review
Multiple research articles have been published about organ and tissue donation. The donation rate is usually tied to social and community factors. Many studies reviewed the effect of preexisting notions about donation. Factors affecting the outcomes that were analyzed included religion, ethnicity, and level of education (3,4). Many people have negative attitudes toward donation given their cultural, ethnic, or religious background. That affects the number of donors and contributes to an indirect increase in the waiting list volume. Those cases are the portion constituting the no authorization section of the outcomes in this study.
The relationship between the hospital and the donation rate, also called the conversion rate, was carefully studied. Great conversion-rate hospitals usually have 85% of the cases become donors, while ineffective conversion-rate hospitals convert as little as 53 percent (5). Many hospital-related factors affect the conversion rates, including whether the hospital is teaching or non-teaching, has trauma level departments, and its size. The urbanity of the hospital location, the quality of its ICU, and whether the patient died from a stroke also significantly affect the outcome (6). Other studies demonstrated the importance of an available hospital-affiliated transplant to the conversion rate (7). However, little to no research studied CNR cases and how they could be predicted or successfully converted to donors. The main focus in organ donation is related to clinical outcomes of transplanted organs rather than donation outcomes.
Similar to other healthcare applications, machine learning (ML) and artificial neural networks (ANN) have been applied to organ donation and transplants. For instance, machine learning has been applied to donor and recipient data to determine the graft survival of multiple organs. A study to predict and improve the organ sharing and survival of a heart transplant used a non-linear artificial neural network with regression and simulation to build a model. The data used was fairly big, like most ANN and ML applications in healthcare (8). However, the most used methodologies in predicting survival are Cox regression and multivariate statistical analysis. Those methods are often combined with specific ANN algorithms such as multiple perceptrons (MLP) and Ada boost in transplant prediction models (9).
In an attempt to build an organ-donation prediction model from outcomes, ML and ANN were used, but the model did not attempt to predict the results of consent. Research exploring the effect of irreversible brain damage on organ donation showed great adaptability to the complex nature of the data. However, no extensive documentation was provided on which algorithms were used and how their performance compares (10).
Similar data from the same organization was reviewed to predict organ donation potential based solely on a neural network approach. A particularity discussed in this research was time series forecasting, given that the analysis depends on a time factor. The research combined time slots with the number of hidden neurons (HN) to serve as the basis for comparing multiple scenarios. The performance of several algorithms was evaluated in (11), which showed radial basis function network (RBFN), committee neural networks (CNN), and backpropagation (BP) performed the best.
Methods
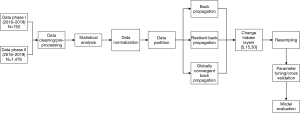
This research aims to predict if potential donation cases will result in organ donation or no recovery of organs. Three network paradigms, all variants of the backpropagation algorithm, were explored. The neural networks chosen to conduct this research have essential predictive abilities and the capability to model complex and non-linear relationships. Figure 2 describes the high-level process map of the methodology adopted for this research.
Data description
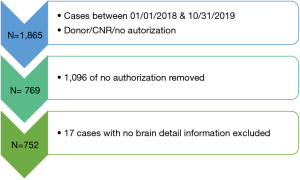
The dataset for this study was extracted using SQL queries from an OPO’s database. All the analysis carried out was applied using R statistical software. The dataset has 1,865 referral cases (BD and DCD), collected from 01/01/2018 to 10/31/2019, including all three outcomes (Donor, CNR, No Authorization). For this study, CNR organs are defined as potential donations that are not recovered from the body despite consent and also organs that could be collected but not used for various reasons. A total of 1,096 cases did not have the authorization, and 17 cases had missing information, as shown in Figure 3.
As a result, the final dataset has 752 cases for donor and CNR outcomes. Sixteen variables, shown in Table 1, were considered for the first phase. The second dataset consisted of 3,685 referred cases to the OPO from 01/01/2016 to 10/31/2019. The aim was to check if a more extensive dataset from a longer period could affect the best-performing neural network model or alter the conclusions from the first dataset. The same filtering technique was applied, which resulted in 1,476 donor and CNR cases. Moreover, new variables were considered for this phase, most of which are related to the referral process and donor characteristics. The variables considered in both phases included donor demographics, medical history, and process-related data as advised by organ procurement professionals. This variation was chosen to include as much pertinent information (medical and non-medical) related to the case. Therefore, determine if there are overlooked or unusual factors that could correlate with the CNR outcome.
Table 1
| Variables | Type | Levels | % missing values |
|---|---|---|---|
| Age | Continuous | – | 0.0% |
| Sex (M/F) | Categorical | 2 | 0.0% |
| Race (Asian, Black, Hispanic, White, other) | Categorical | 5 | 0.0% |
| Cause of death (anoxia, stroke, trauma, other) | Categorical | 4 | 0.0% |
| Body mass index (BMI) | Continuous | 2.7% | |
| Clinical trigger met (0=no, 1=yes) | Categorical | 2 | 0.0% |
| Potential donor type (organ, organ/eye, organ/tissue, organ/tissue/eye) | Categorical | 4 | 0.0% |
| Time from clinical trigger to referral (h) | Continuous | – | 3.6% |
| Time from referral to approach (h) | Continuous | – | 0.7% |
| Time from death to approach (h) | Continuous | – | 25.7% |
| Time from grave prognosis to approach (h) | Continuous | – | 5.2% |
| Time from initial mention to approach (h) | Continuous | – | 26.6% |
| Organ detail | Categorical | 10 | 0.0% |
| Brain detail | Categorical | 4 | 0.0% |
| Trigger timely (0=no, 1=yes) | Categorical | 2 | 0.0% |
| Organ outcome (donor, CNR) | Categorical | 2 | 0.0% |
CNR, consented but not recovered.
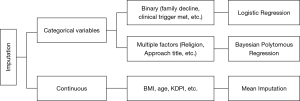
As shown in Table 1, most of the variables did not have missing values, and none missed more than 27%, which permits data imputation. Data imputation was carried out using predictive mean matching. This approach considers the existing values of all the variables to predict the missing values in the dataset. After assigning possible candidates for each missing data point, all scenario combinations are explored to determine which values better predict the outcome variable (i.e., organ outcome). The prediction, in this case, was performed using the random forest machine learning algorithm and was applied for 5 iterations which indicated the number of multiple imputations taken into consideration (11). Normalization was performed on the continuous variables to avoid any scaling effect on the models.
For the second dataset, the missing values occurred in continuous and categorical variables. The imputation approach was slightly modified to accommodate categorical values imputation as represented in Figure 4. The continuous variables were imputed similarly to dataset 1 through random forest predictive mean matching. Categorical variables in dataset 2 were in the form of binary and multi-level variables. For the first type, logistic regression was applied to impute the missing values, while for the second type, a Bayesian polytomous regression was conducted.
Artificial neural networks
Three artificial neural network paradigms were applied to the dataset. Bprop is known for its performance in supervised learning for classification tasks. Furthermore, Bprop constitutes the base model for this study because of its robust nature and its error accountability feature. The other models are resilient propagation (Rprop) and globally convergent propagation (Gprop), which are modified versions of Bprop that aim to overcome some of its shortcomings.
A backpropagation network is one of the main structures proved to be highly robust in prediction using neural networks. Unlike other algorithms, backpropagation controls errors by resubmitting flawed solutions to the initial neurons, allowing the backpropagation method to improve in the next iteration. Similar to the basic notion of neural networks, backpropagation relies on the parameter as well as the input, including the threshold, learning rate, and momentum. Those could be changed depending on the application and the number of neurons. Therefore, the model should be calibrated correctly to achieve optimal results and for better application and functioning of the algorithm.
The resilient propagation network is directly derived from backpropagation and holds the general algorithm properties except for some differences. Rprop generally results in a faster convergence time compared to other neural network methodologies. Although it can be more complex to implement, it was proven to be more accurate than Bprop. Furthermore, its convergence properties help eliminate weight stagnation around the local minima. Unlike backpropagation, Rprop has a particular way to update the weights, which constitutes the main difference between the two algorithms. Bprop calculates the update based on the magnitude of the partial derivative, while the Rprop calculates a delta for every connection, and based on that, the size of the weight update is determined where the error gradient from a previous iteration is considered. The delta is calculated as following (see Eq. [1]) (12).
The globally convergent propagation network is mainly based on the quick propagation methodology performed by feedforward neural networks, particularly for batch training. However, it has issues related to minimizing error surfaces and stability related to adapting incorrect learning rates. Usually, several heuristic methods are applied to the learning rate to attempt to overcome those issues. The globally convergent theorem presents a modified algorithm that improved speed convergence of quick propagation while preserving its stability (13).
Root mean square error (RMSE), mean absolute error (MAE), and the sum of squared error (SSE) were used to evaluate the performance of the three networks. RMSE, a commonly used measure, quantifies the difference between predicted yi and actual values zi based on quadratic scoring (see Eq. [2]). MAE measures the difference between predicted and actual values without considering the error direction (see Eq. [3]). SSE measures the variation within the predicted values with respect to the mean predicted value (see Eq. [4]) (14).
Statistical analysis
Phase I
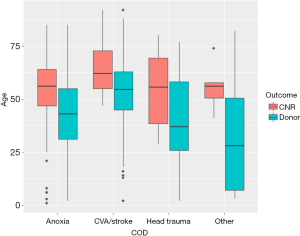
The first step was to explore the factors’ statistical relationships to understand the intrinsic characteristics of the given data. Out of all investigated relationships, the relationship between age, cause of death, and the outcome stood out. As illustrated in Figure 5, among all ages, CNR cases are more likely to occur in the older age group. Those patients likely present health complications that could reduce the quality of their organs.
Phase II
The second phase replicated the same methodology applied to the first dataset. The investigation of the data resulted in the summary provided in Table 2. The 4 factors that are reported represent the main variables that summarizes the demographics. The data in this part of the analysis was obtained before applying the filtering and the imputation described in previous sections
Table 2
| Variables | Group | Frequency | Percent (%) |
|---|---|---|---|
| Gender | F | 1,544 | 41.9 |
| M | 2,141 | 58.1 | |
| Age (years) | 0–17 | 202 | 5.5 |
| 18–34 | 592 | 16.1 | |
| 35–49 | 800 | 21.7 | |
| 50–64 | 1,338 | 36.3 | |
| 65–75 | 452 | 12.3 | |
| 76+ | 301 | 8.2 | |
| Cause of death | Anoxia | 1,900 | 51.6 |
| CNS tumor | 16 | 0.4 | |
| CVA/stroke | 1263 | 34.3 | |
| Head trauma | 433 | 11.8 | |
| Other | 73 | 2 | |
| Race | Asian | 336 | 9.1 |
| African American | 954 | 25.9 | |
| Hispanic | 957 | 26 | |
| Other | 10 | 0.3 | |
| Caucasian | 1,428 | 38.8 |
CNS, central nervous system; CVA, cerebrovascular accident; F, female; M, male.
The summary shows that CNR cases are dominated by male potential donors (58.1%) and patients admitted for anoxia (51.6%). The most relevant race is Caucasian (38.9%) followed by African American (25.9%). For the age groups, the most dominant age for CNR cases is from 50 to 64 years old (36.3%), which can be attributed to the quality of the organs.
To evaluate the impact on occurrences of specific clinical measures in terms of the organ outcome, these factors were reported with regards to the three outcomes (Donor, CNR, and no authorization) as shown in Table 3. Of the 92.7% of the CNR cases that met the donor service area definition, almost all of them (98.9%) were not potential donations. Of those that met the definition, 42 percent were ruled out for medical reasons. These CNR cases don’t usually meet the set clinical trigger (39.5%) where the organ trigger is not timely (58%).
Table 3
| Factor | Levels | CNR | Donor | No authorization | |||||
|---|---|---|---|---|---|---|---|---|---|
| # | % | # | % | # | % | ||||
| Organ trigger timely | No | 215.0 | 58.0 | 743.0 | 64.1 | 1,252.0 | 58.1 | ||
| Yes | 156.0 | 42.0 | 416.0 | 35.9 | 903.0 | 41.9 | |||
| Clinical trigger met | No | 13.0 | 3.5 | 16.0 | 1.4 | 72.0 | 3.3 | ||
| Yes | 358.0 | 96.5 | 1,143.0 | 98.6 | 2,083.0 | 96.7 | |||
| Meet DSA definition | No | 27.0 | 7.3 | 49.0 | 4.2 | 391.0 | 18.1 | ||
| Yes | 344.0 | 92.7 | 1,110.0 | 95.8 | 1,764.0 | 81.9 | |||
| Organ detail | Appears BD | 0.0 | 0.0 | 0.0 | 0.0 | 664.0 | 30.8 | ||
| BD | 0.0 | 0.0 | 0.0 | 0.0 | 853.0 | 39.6 | |||
| Cardiac arrest | 37.0 | 10.0 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| DCD | 115.0 | 31.0 | 194.0 | 16.7 | 638.0 | 29.6 | |||
| ECD | 0.0 | 0.0 | 310.0 | 26.7 | 0.0 | 0.0 | |||
| General | 8.0 | 2.2 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| Intra-Op | 23.0 | 6.2 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| ME decline | 4.0 | 1.1 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| MRO | 156.0 | 42.0 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| MSOF | 4.0 | 1.1 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| NBD | 24.0 | 6.5 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| SCD | 0.0 | 0.0 | 655.0 | 56.5 | 0.0 | 0.0 | |||
| Organ potential | No | 367.0 | 98.9 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Yes | 4.0 | 1.1 | 1,159.0 | 100.0 | 2,155.0 | 100.0 | |||
| Blood type | A | 108.0 | 29.1 | 374.0 | 32.3 | 419.0 | 19.4 | ||
| AB | 21.0 | 5.7 | 38.0 | 3.3 | 81.0 | 3.8 | |||
| B | 66.0 | 17.8 | 167.0 | 14.4 | 237.0 | 11.0 | |||
| O | 166.0 | 44.7 | 580.0 | 50.0 | 655.0 | 30.4 | |||
| Other | 10.0 | 2.7 | 0.0 | 0.0 | 763.0 | 35.4 | |||
BD, brain dead; CNR, consented but not recovered; DCD, donor from cardiac death; ECD, extended criteria donor; ME, medical examiner; MRO, medical rule out; MSOF, multi-system organ failure; NBD, not brain dead; SCD, standard criteria donor; DSA, donor service area.
Results
Prediction results
Phase I
Around 85% of the data was used for training, 15 percent for testing, and randomly assigned data to fill the splits. All three models were designed at 3 different values of hidden neurons (5, 15, and 30). All the models were cross-validated through iterative random sampling of the training and testing while keeping the hyperparameters of the original models constant. For Rprop and Gprop, a vector for the multiplication factor of the learning rate was specified at values between 0.5 and 1.2 for all iterations. The threshold that refers to the stopping criteria of the error function from the partial derivative was fixed at 0.01, applicable to all scenarios.
Table 4 shows that the resilient propagation model performed better on the training dataset when the number of hidden neurons was increased from 5 to 15. For the testing dataset, the model showed better results for 5 and 30 hidden neurons.
Table 4
| HN | Train | Test | |||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | SSE | RMSE | MAE | SSE | ||
| 5 | 0.100 | 0.050 | 4.330 | 0.160 | 0.040 | 4.320 | |
| 15 | 0.030 | 0.003 | 1.240 | 0.420 | 0.070 | 6.120 | |
| 30 | 0.030 | 0.003 | 1.240 | 0.170 | 0.040 | 4.350 | |
HN, hidden neurons; RMSE, root mean square error; MAE, mean absolute error; SSE, sum of squared error.
For the Bprop model, the learning rate was set at 0.0001 while keeping all other hyperparameters constant. The activation function was the logistic function. Table 5 shows that the backpropagation model performed better on the training dataset when using 30 hidden neurons. The testing dataset errors were lower when 5 and 30 hidden neurons were used.
Table 5
| HN | Train | Test | |||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | SSE | RMSE | MAE | SSE | ||
| 5 | 0.050 | 0.005 | 2.210 | 0.100 | 0.040 | 4.320 | |
| 15 | 0.060 | 0.010 | 2.520 | 0.200 | 0.050 | 4.650 | |
| 30 | 0.020 | 0.003 | 0.250 | 0.100 | 0.040 | 4.370 | |
HN, hidden neurons; RMSE, root mean square error; MAE, mean absolute error; SSE, sum of squared error.
The globally convergent propagation model performed better on the training dataset for 30 hidden neurons with similar hyperparameters. The testing errors indicate similar results when 5 and 30 hidden neurons were used, as shown in Table 6.
Table 6
| HN | Train | Test | |||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | SSE | RMSE | MAE | SSE | ||
| 5 | 0.070 | 0.007 | 3.140 | 0.210 | 0.050 | 5.150 | |
| 15 | 0.040 | 0.004 | 1.210 | 0.240 | 0.060 | 6.940 | |
| 30 | 0.010 | 0.002 | 0.200 | 0.220 | 0.050 | 5.510 | |
HN, hidden neurons; RMSE, root mean square error; MAE, mean absolute error; SSE, sum of squared error.
Comparing the training errors of the three models on predicting the donation outcomes, Gprop performs marginally better than Bprop and Rprop when 30 hidden neurons were used. Hence, the Gprop was used to rank the variables based on their order of importance on donation outcomes.
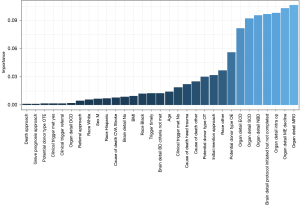
Figure 6 shows that the best indicative variable of the outcome is when the case is a medical rule out (MRO), and the least important variable in determining the outcome is the time difference between death and approach, as well as the time between grave prognosis and approach. The variables that showed no importance are not included in the figure. The MRO and medical examiner decline might be a prominent predictor of the CNR; however, it is a fact that is only known later on in the process. As part of improving the model, only the other predictors will be considered to predict the occurrence of CNR. The figure shows that a not brain-dead case with organ and eye donor potential can be solid predictors in this specific data, while the time between approach and death is the least significant predictor.
Phase II
For the modeling in this part, accuracy and the RMSE measure used previously to evaluate the performance are reported. The number of epochs, hidden neuron variation, and model parameters was kept constant.
Table 7 shows the results from the second phase analysis. The three models were evaluated in terms of Accuracy and RMSE. Interestingly, the results from phase 2 are very similar to phase I. Comparing scenarios from each model from the three variations of neurons, Gprop at 30 hidden neurons performed the best. The worst scenario among all the models was Rprop at 5 hidden neurons. Therefore, considering a slightly bigger dataset does improve the accuracy but does not change the model type that performs the best.
Table 7
| Metrics | Bprop | Rprop | Gprop | |||||
|---|---|---|---|---|---|---|---|---|
| Best Scenario | Worst Scenario | Best Scenario | Worst Scenario | Best Scenario | Worst Scenario | |||
| Accuracy | 0.65 | 0.53 | 0.69 | 0.38 | 0.80 | 0.64 | ||
| RMSE | 0.42 | 0.62 | 0.31 | 0.59 | 0.15 | 0.49 | ||
RMSE, root mean square error.
This analysis creates the basis for a decision support system that will serve as a helpful tool for the organ donation and transplant staff when dealing with such cases. It provides an insight into the likelihood of a case being a donor or CNR. This knowledge at the start of a case can be highly advantageous to allow the medical and donation team to focus their effort on donor cases where the recovery is most probable. These initial results also present the factors that can be major predictors for such outcomes. In our analysis, process-related variables, as well as donor characteristics, were involved. The initial results suggest that it is always related to a medical rule out as well as not brain-dead cases. On the other hand, the factor with the least predictive power was the time between death and approach.
Conclusions
This study aimed to predict the likelihood of a consented, not recovered case for organ donation. A total of 752 CNR and donor cases received by the OPO over 22 months were investigated for the first phase. In addition, 1,476 CNR and donor cases spanning 4 years were analyzed in the second phase. Multiple data transformations and structuring techniques were used to preprocess the available data. Three neural network approaches, backpropagation, resilient propagation, and globally convergent propagation, were implemented. The best model was Gprop, with 30 hidden neurons for both phases. The output of Gprop suggested medical rule out was the most important factor and the time from the donor’s death to the approach was the least important factor in donation outcomes. Medical rule out is a significant predictor because it indicates that an underlying medical condition made the organs unsuitable for donation. The results from this research could help the OPO better understand the dynamics of CNR cases and what directly affects them. For future work, committee networks and other predictive modeling approaches could be explored. Moreover, further diversification of the variables used to train the model can be of high importance.
Acknowledgments
Funding: None.
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at https://jmai.amegroups.com/article/view/10.21037/jmai-21-9/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jmai.amegroups.com/article/view/10.21037/jmai-21-9/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Organ Procurement and Transplantation Network, “OPTN Data,” Organ Procurement and Transplantation Network. (Online). Available online: https://optn.transplant.hrsa.gov/ (Accessed: December 1, 2019).
- United Network for Organ Sharing, “UNOS: US Organ Transplantation,” UNOS. (Online). Available online: https://unos.org/ (Accessed: December 7, 2019).
- Sadrawi M, Shieh J. S, Abbod M. Self-Adaptive Neural Networks Applied to Brain Death Function Level Prediction. Proceedings of 2013 Annual International Scholars Conference. 2013:216-214.
- Haydon GH, Hiltunen Y, Lucey MR, et al. Self-organizing maps can determine outcome and match recipients and donors at orthotopic liver transplantation. Transplantation 2005;79:213-8. [Crossref] [PubMed]
- Reinaldo F, Fernandes C, Rahman MA, et al. Assessing the eligibility of kidney transplant donors. In: International Workshop on Machine Learning and Data Mining in Pattern Recognition 2009:802-809.
- Mostafa MM. A psycho-cognitive segmentation of organ donors in Egypt using Kohonen’s self-organizing maps. Expert Systems with Applications 2011;38:6906-15. [Crossref]
- Nilsson J, Ohlsson M, Höglund P, et al. The International Heart Transplant Survival Algorithm (IHTSA): a new model to improve organ sharing and survival. PLoS One 2015;10:e0118644. [Crossref] [PubMed]
- Shouval R, Labopin M, Unger R, et al. Prediction of Hematopoietic Stem Cell Transplantation Related Mortality- Lessons Learned from the In-Silico Approach: A European Society for Blood and Marrow Transplantation Acute Leukemia Working Party Data Mining Study. PLoS One 2016;11:e0150637. [Crossref] [PubMed]
- Torres L, Vicente H, Novais P, et al. Prediction of organ donation after irreversible brain damage. In: Proceedings of the 2014 International Conference on Future Communication Technology and Engineering 2015:333.
- Schleich BR, Lam SS, Yoon SW, et al. A Neural Network-based Approach for Predicting Organ Donation Potential. In: Institute of Industrial and Systems Engineers Annual Conference. Proceedings 2013:1532.
- Musil CM, Warner CB, Yobas PK, et al. A comparison of imputation techniques for handling missing data. West J Nurs Res 2002;24:815-29. [Crossref] [PubMed]
- Prasad N, Singh R, Lal SP. Comparison of back propagation and resilient propagation algorithm for spam classification. In: 2013 Fifth International Conference on Computational Intelligence, Modelling and Simulation 2013:29-34.
- Vrahatis MN, Magoulas GD, Plagianakos VP. Globally convergent modification of the quickprop method. Neural Processing Letters 2000;12:159-70. [Crossref]
- Gramatica P, Sangion A. A Historical Excursus on the Statistical Validation Parameters for QSAR Models: A Clarification Concerning Metrics and Terminology. J Chem Inf Model 2016;56:1127-31. [Crossref] [PubMed]
Cite this article as: Ghali H, Lam SS, Carpini KD, Ezzell C, Friedman AL, Yoon S, Won D. Neural network-based prediction of consented organs utilization. J Med Artif Intell 2022;5:1.