
Approximating femoral neck bone mineral density from hand, knee, and pelvis X-rays using deep learning
Highlight box
Key findings
• Low BMD at the femoral neck (used to diagnose bone loss and fracture risk) can be opportunistically screened from routinely acquired X-rays of the hand, knee, or pelvis, i.e., even when the femoral neck is not included in the field of view.
What is known and what is new?
• Screening for low BMD from conventional X-rays has the potential to improve patient care.
• This manuscript presents an algorithm that can opportunistically identify patients with low BMD at the femoral neck without the need for segmentation or feature extraction.
What is the implication, and what should change now?
• Opportunistic screening for low BMD from conventional X-ray could help address the known care gap in osteoporosis management, i.e., under-screening and under-diagnosis. Radiologists can include a finding of suspected low BMD in their X-ray report to encourage referring physicians to conduct a clinical fracture risk assessment and refer their patient for DXA if appropriate.
Introduction
Background
Osteoporosis affects 200 million lives globally (1). The prevalence of osteoporosis in the US, in adults over the age of 50 years is 15% and 4% in women and men, respectively, and its incidence and prevalence are rising with the aging population (2). In their lifetime, 50% of women and 22% of men will suffer an osteoporotic fracture (3), and of patients who suffer an osteoporotic hip fracture, 30% die within 1 year (4). Osteoporosis is underdiagnosed (5) and preventable. If at-risk patients are identified, pharmacologic therapy and lifestyle modifications can decrease fracture risk by 70% within 1 year of initiation (6). Currently, osteoporosis is diagnosed by dual-energy X-ray absorptiometry (DXA). The United States Preventive Services Task Force (USPSTF) recommends bone mineral density (BMD) testing by DXA in women 65 and older, and younger women with certain clinical risk factors (7). Despite the recommendations, screening rates are low. In a study of over 1.6 million privately insured women, fewer than 25% of those over 65 years were screened (8). There are no recommendations for screening men, despite their higher mortality following an osteoporotic fracture (7,9). An opportunistic screen for low BMD from X-ray could alert a care provider to conduct a clinical fracture risk assessment, and refer for DXA if appropriate.
Rationale and knowledge gap
DXA is the gold standard approach to accurately measure BMD, and it achieves that by using X-rays at two energies to subtract the confounding soft-tissue X-ray attenuation from the overall attenuation. Multiple approaches have been proposed to classify osteoporosis or estimate BMD from X-ray images (10-14) but a simple model, without need for manual feature extraction, that could be implemented opportunistically, and that could operate on X-rays of multiple anatomical locations has yet to be developed.
Objective
Our objective was to train a deep convolutional neural network (CNN) (15) to learn the complex features of bone and soft tissue attenuation to estimate BMD from standard hand, knee, and pelvis X-rays. Such a tool has the potential to opportunistically screen for low BMD in individuals that undergo hand, knee, or pelvis X-rays for any clinical indication, which in turn could empower patients and their providers to initiate preventative treatment.
Methods
This retrospective study proposes a deep learning (DL)-based model to predict femoral neck BMD, in order to classify patients as having low BMD, from X-rays of either hand, knee, or pelvis, and the patient’s sex and age. Femoral neck BMD will be referred to as BMD hereafter.
Dataset
A publicly available dataset collected as part of the Osteoarthritis Initiative (OAI) (16) was used. The OAI dataset (17) includes data from the multicenter, longitudinal study of 4,796 participants, 1,396 with symptomatic knee osteoarthritis (OA) of at least one knee, 3,278 with increased risk of developing symptomatic OA, and 122 without knee OA or other risk factors. Recruitment began in 2004, and the study was completed in 2011. Participants ranged in age from 45 to 79 years at the time of enrollment, and had fixed flexion radiographs of the hand, knee, and pelvis. A subset of participants had repeated X-rays at 1 or 2 years after baseline. The OAI was conducted in accordance with the Declaration of Helsinki defined in the 1964 and meets all amendments made after. OAI was approved by each site’s IRB: Memorial Hospital of Rhode Island (Pawtucket, RI, USA) Ohio State University (Columbus, OH, USA), University of Pittsburgh (Pittsburgh, PA, USA), and University of Maryland/Johns Hopkins University (Baltimore, MD, USA) and at the coordinating center (University of California, San Francisco, CA, USA; approval number 10-00532). All participants provided informed consent prior to participation. A de-identified subset of OAI data was used in this study for model development and testing, which included all available records of X-ray/DXA pairs (n=1,742) from 771 DXA exams coming from 533 unique patients (51% male). All these patients came from the progression subcohort, meaning they had symptomatic tibiofemoral knee OA at baseline, both of the following in at least one knee at baseline: frequent knee symptoms in the past year, and radiographic tibiofemoral knee OA. Patients ranged in age from 48 to 83 years at the time of image acquisition. The prevalence of low BMD (T-score <−1) and osteoporosis (T-score <−2.5) vs. the general population was lower in males (27% and 1%, respectively, vs. 39 and 4%) and in females (52% and 3%, respectively, vs. 66% and 15%) (2). Table 1 summarizes the characteristics of the subjects in the cohort.
Table 1
| Characteristics | Hand | Knee | Pelvis |
|---|---|---|---|
| Number of unique patients | 542 | 602 | 531 |
| Number of unique DXA exams | 890 | 3,614 | 661 |
| Sex (male/female), n | 280/262 | 302/300 | 272/259 |
| Age (years), mean (SD) | 65.0 (9.4) | 64.5 (9.3) | 65.0 (9.3) |
| Femoral neck BMD (g/cm2), mean (SD) | 0.95 (0.15) | 0.96 (0.15) | 0.95 (0.15) |
| BMD status (normal/low), n | 531/359 | 2,224/1,390 | 396/265 |
Number of unique DXA exams is greater than unique patients as (I) some patients had X-ray and/or DXA acquired multiple time points; and (II) images were split into two images (left and right) and considered separately. BMD status: low if T-score <−1. DXA, dual-energy X-ray absorptiometry; SD, standard deviation; BMD, bone mineral density.
Data provided by OAI included age, sex, height, weight, ethnicity, fixed flexion, plus some additional co-variate data (such as trabecular thickness, trabecular number, intact PTH level, 25-vitamin D level, trabecular spacing, and bone volume fraction), as well as radiographs of the hand, knee, and/or pelvis, and DXA-derived values for BMD, which is used as the ground truth. BMD was measured using identical Lunar Prodigy Advance systems (GE Lunar Corp., Madison, WI, USA) at each institution. BMD values from Lunar systems were converted to a Hologic base using clinically accepted methods.
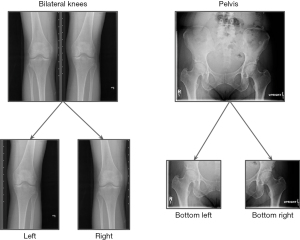
Two different approaches were used to increase the number of samples. First, the bilateral hand and knee images are split into two separate left and right images, and the same BMD was used as the ground truth target for both images. This was also applied to the pelvis by splitting the X-ray into lower-left and lower-right images (see Figure 1 for an example). Second, a fixed-length time window, t, was chosen around the date of a patient’s hip DXA exam, and the DXA BMD served as the target for all the X-rays taken within that window. The value of t was treated as a hyper-parameter and its best value was found through an optimization process.
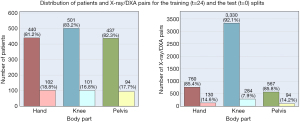
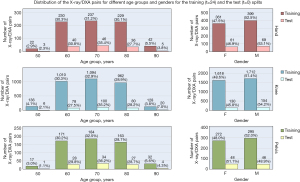
The dataset was first split into separate body part datasets, and then each was split into training and test sets on a per-patient basis, using stratified random sampling by sex and age decade to ensure that each set had female composition and equal distribution by age decade. In the experiments, the training and test sets had 80% and 20% of the patients, respectively. The training set goes through a k-fold cross validation process, and the validation splits are used for final model tuning. Figures 2,3 show the distributions of patients and their age group and sex in the training and the test splits.
Proposed model
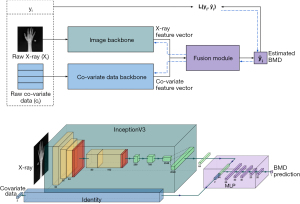
The proposed model architecture consisted of the image and the co-variate data backbones to respectively encode the raw X-ray images xi, and the co-variate data ci (i.e., age and sex). Intuitively, the backbones were feature extraction modules, whose weights were learned throughout the end-to-end training of the entire model. The extracted features were then combined to form the final vector from which the BMD was estimated. This was done through a fusion module, which was a regression head.
The following implementation of this architecture demonstrated the best performance in the experiments:
- Image backbone was an InceptionV3 model pre-trained on ImageNet with the classification layer replaced by a fully-connected layer of size 64.
- The co-variate data backbone was the identity block. This means that the co-variate data were directly fed to the fusion module.
- The fusion module received the concatenation of the two inputs of size 66 (64+2) and fed them to a multi-layer perceptron (MLP) architecture of 5 fully-connected hidden layers and rectified linear unit (ReLU) activation functions.
The details of the architecture and implementation of the model are presented in Figure 4. Additional details can be found in Appendix 1.
Three independent training bundles (one for each body part) were used to train the proposed model. Each model was trained using the k-fold cross validation technique over patients (stratified by sex and age decade), with k=5. The window size was set to t=0 for the validation and test splits. The best model of each fold was selected based on the average L1 error of the validation split of that fold. Therefore, the final model was an ensemble of k models, which was then evaluated on the test split.
The input images were initially resized to (w × h)/0.9, and then random horizontal flips followed by a random crop of 90% of the image (yielding w × h crops) were applied as augmentation steps. Age of the patients were divided by 100 and sex is encoded using binary encoding.
The loss function was chosen to be mean absolute error (MAE) as it is one of the most common choices for regression problems. The network weights were optimized using Adam optimizer with the step learning rate scheduler.
Statistical analysis
T-scores were derived from BMD values using female peak bone mass from National Health and Nutritional Examination Surveys (NHANES) III (18). Area under the receiver operating characteristic (ROC) curve (AUROC) was employed to assess the “low BMD” (yes/no DXA T-score <−1) classification performance. Algorithm-derived (predicted) T-score thresholds were chosen based on the ROC curves computed using the validation split of each fold.
The predicted BMD of the test set was calibrated using the k-fold cross-validation technique (19), and the T-scores were derived as described above. In the test sets, model performance at estimating continuous BMD vs. DXA ground truth were assessed with Passing-Bablok (20) and Bland-Altman (21). AUROC, accuracy, sensitivity, and specificity were employed to assess the “low BMD” (DXA T-score <−1) classification performance at the algorithm-derived T-score thresholds obtained from the validation splits. Given the sex difference in the prevalence of low BMD (2), performance was assessed in males and females, separately. The R package cutpointr (22) was used to calculate the 95% confidence intervals on the area under the curve (AUC) using 4,000 bootstraps using in-bag values in the AUC_b column of the bootstrap results.
Results
Three independent training bundles, one for each body part, as well as three other baselines that were trained on all the co-variate data are presented below. Intuitively, the goal was to emphasize the positive impact of the features extracted from the X-ray images of different body parts through the proposed model, alongside the age and sex features. The four different categories of models with which we experimented were:
- Baseline: group aggregation (BaseGA): BMD aggregation was applied on different age and sex combination groups. The resulting look-up table was applied on the samples in the test dataset to estimate BMD.
- Baseline: regression (BaseBG): the best of the three different regression approaches of linear regression, Bayesian ridge regression, and support vector regression with RBF kernel was selected.
- Baseline: decision tree (BaseDT): a model based on gradient boosting (23) was trained and the results were reported on the test split.
- Proposed DL model: the network weights were initialized using ImageNet pre-trained weights, the image size is set to 1,024×1,024 for the hand model, and to 512×512 for the knee and pelvis models. All models were trained for 3,000 epochs using a 24-month window size, with the learning rate initialized at 0.0008 and decreased to 0.00008 after 2,000 epochs.
BMD estimation performance
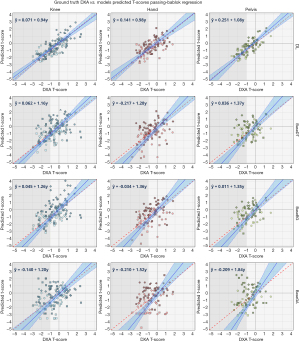
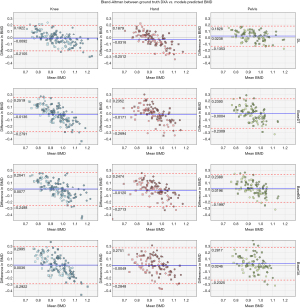
As presented in Figure 5, the DL model shows superior performance with the highest correlation between ground truth and predicted BMDs, lower standard errors, and narrower 95% confidence compared to all the baselines. Notably, all the knee models show better performance than the other body parts, which is hypothesized to be due to larger dataset size. The agreement analysis inferred by the Bland-Altman regression plots in Figure 6 show that all the DL models have better agreement with the ground truth as depicted by the limit lines (−0.25 to −0.19 g/cm2 for hand, −0.21 to −0.19 g/cm2 for knee, and −0.14 to −0.18 g/cm2 for pelvis), compared to those of the baseline models. Furthermore, while the agreement mean (blue line in the figure) is almost the same for all the baselines and the DL model, it is clear that the baseline model predictions are slightly more biased than the DL model. The bias is lowest on the DL model for pelvis, and it demonstrates the highest confidence (with limits of agreement being between −0.14 to −0.18 g/cm2). Mean differences of all the knee models are closer to the zero line, which is hypothesized to be due to the larger dataset size.
Low BMD diagnostic performance
The classification results are summarized in Tables 2-4 for the hand, knee, and pelvis models, respectively. The optimal T-score cut-off (lower false positive rate vs. higher true positive rate) are calculated directly from the ROC curve of each model, from which the predicted classification label (diagnosis) is assigned to the test samples, and further classification metrics are evaluated thereafter. The results show dominant performance of the DL model over the baselines on all of the classification metrics. There is a sizable difference between the DL model AUC and that of the baseline models for all of the body parts, with the exception of female hands, which results in superior accuracy, sensitivity, and specificity of the DL model.
Table 2
| Classification results | BaseGA | BaseBG | BaseDT | DL | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| F | M | F | M | F | M | F | M | ||||
| AUC | 0.70 (0.58 to 0.82) | 0.49 (0.34 to 0.64) | 0.78 (0.67 to 0.88) | 0.78 (0.67 to 0.89) | 0.83 (0.72 to 0.92) | 0.71 (0.57 to 0.83) | 0.86 (0.76 to 0.94) | 0.82 (0.72 to 0.91) | |||
| T-score cut-point | −1.38 | 0.33 | −1.37 | −0.16 | −1.20 | −0.17 | −0.80 | −0.35 | |||
| True positive | 15 | 9 | 17 | 11 | 18 | 10 | 18 | 12 | |||
| True negative | 18 | 19 | 20 | 24 | 22 | 22 | 22 | 25 | |||
| False positive | 9 | 16 | 7 | 11 | 5 | 13 | 5 | 10 | |||
| False negative | 8 | 8 | 6 | 6 | 5 | 7 | 5 | 5 | |||
| Accuracy | 0.66 (0.54 to 0.76) | 0.54 (0.42 to 0.65) | 0.74 (0.64 to 0.84) | 0.67 (0.56 to 0.79) | 0.80 (0.70 to 0.88) | 0.62 (0.50 to 0.73) | 0.80 (0.70 to 0.90) | 0.71 (0.62 to 0.81) | |||
| Sensitivity | 0.65 (0.48 to 0.81) | 0.53 (0.33 to 0.73) | 0.74 (0.58 to 0.88) | 0.65 (0.45 to 0.83) | 0.78 (0.64 to 0.91) | 0.59 (0.38 to 0.79) | 0.78 (0.64 to 0.91) | 0.71 (0.50 to 0.89) | |||
| Specificity | 0.67 (0.52 to 0.81) | 0.54 (0.40 to 0.69) | 0.74 (0.60 to 0.88) | 0.69 (0.55 to 0.81) | 0.81 (0.68 to 0.93) | 0.63 (0.50 to 0.76) | 0.81 (0.68 to 0.93) | 0.71 (0.58 to 0.83) | |||
Total number of patients: 102 (M: 52, F: 50). 95% CIs are shown in brackets. BaseGA, baseline group aggregation; BaseBG, baseline basic regression; BaseDT, baseline decision tree; DL, deep learning; F, female; M, male; AUC, area under the curve; CI, confidence interval.
Table 3
| Classification results | BaseGA | BaseBG | BaseDT | DL | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| F | M | F | M | F | M | F | M | ||||
| AUC | 0.69 (0.57 to 0.80) | 0.55 (0.42 to 0.69) | 0.83 (0.74 to 0.90) | 0.80 (0.71 to 0.88) | 0.78 (0.68 to 0.87) | 0.77 (0.66 to 0.86) | 0.87 (0.79 to 0.94) | 0.89 (0.82 to 0.95) | |||
| T-score cut-point | −0.98 | 0.22 | −1.04 | −0.30 | −1.07 | −0.26 | −1.21 | −0.71 | |||
| True positive | 17 | 13 | 21 | 17 | 19 | 16 | 21 | 19 | |||
| True negative | 23 | 29 | 28 | 38 | 27 | 34 | 29 | 43 | |||
| False positive | 15 | 24 | 10 | 15 | 11 | 19 | 9 | 10 | |||
| False negative | 10 | 11 | 6 | 7 | 8 | 8 | 6 | 5 | |||
| Accuracy | 0.62 (0.52 to 0.71) | 0.55 (0.45 to 0.64) | 0.75 (0.66 to 0.85) | 0.71 (0.62 to 0.81) | 0.71 (0.62 to 0.80) | 0.65 (0.56 to 0.74) | 0.77 (0.68 to 0.85) | 0.81 (073 to 0.87) | |||
| Sensitivity | 0.63 (0.48 to 0.78) | 0.54 (0.38 to 0.71) | 0.78 (0.64 to 0.90) | 0.71 (0.56 to 0.86) | 0.70 (0.56 to 0.85) | 0.67 (0.50 to 0.83) | 0.78 (0.64 to 0.90) | 0.79 (0.65 to 0.92) | |||
| Specificity | 0.61 (0.47 to 0.73) | 0.55 (0.44 to 0.66) | 0.74 (0.61 to 0.85) | 0.72 (0.61 to 0.82) | 0.71 (0.58 to 0.83) | 0.64 (0.53 to 0.75) | 0.76 (0.64 to 0.87) | 0.81 (0.72 to 0.90) | |||
Total number of patients: 142 (M: 77, F: 65). 95% CIs are shown in brackets. BaseGA, baseline group aggregation; BaseBG, baseline basic regression; BaseDT, baseline decision tree; DL, deep learning; F, female; M, male; AUC, area under the curve; CI, confidence interval.
Table 4
| Classification results | BaseGA | BaseBG | BaseDT | DL | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| F | M | F | M | F | M | F | M | ||||
| AUC | 0.80 (0.68 to 0.91) | 0.54 (0.37 to 0.69) | 0.69 (0.56 to 0.81) | 0.77 (0.64 to 0.88) | 0.70 (0.57 to 0.82) | 0.62 (0.47 to 0.78) | 0.92 (0.85 to 0.97) | 0.88 (0.79 to 0.96) | |||
| T-score cut-point | −0.99 | 0.22 | −0.97 | −0.06 | −1.15 | −0.15 | −0.85 | −0.50 | |||
| True positive | 18 | 9 | 14 | 12 | 16 | 10 | 21 | 13 | |||
| True negative | 19 | 14 | 15 | 21 | 18 | 17 | 21 | 23 | |||
| False positive | 5 | 15 | 9 | 8 | 6 | 12 | 3 | 6 | |||
| False negative | 6 | 8 | 10 | 5 | 8 | 7 | 3 | 4 | |||
| Accuracy | 0.77 (0.67 to 0.88) | 0.50 (0.37 to 0.61) | 0.60 (0.48 to 0.73) | 0.72 (0.61 to 0.83) | 0.71 (0.60 to 0.81) | 0.59 (0.48 to 0.72) | 0.88 (0.79 to 0.94) | 0.78 (0.67 to 0.87) | |||
| Sensitivity | 0.75 (0.60 to 0.89) | 0.52 (0.36 to .067) | 0.58 (0.42 to 0.75) | 0.71 (0.50 to 0.88) | 0.67 (0.52 to 0.82) | 0.59 (0.39 to 0.79) | 0.88 (0.75 to 0.97) | 0.76 (0.58 to 0.93) | |||
| Specificity | 0.79 (0.64 to 0.92) | 0.47 (0.27 to 0.67) | 0.63 (0.46 to 0.79) | 0.72 (0.58 to 0.86) | 0.75 (0.59 to 0.89) | 0.59 (0.43 to 0.74) | 0.88 (0.75 to 0.96) | 0.79 (0.67 to 0.91) | |||
Total number of patients: 94 (M: 46, F: 48). 95% CIs are shown in brackets. BaseGA, baseline group aggregation; BaseBG, baseline basic regression; BaseDT, baseline decision tree; DL, deep learning; F, female; M, male; AUC, area under the curve; CI, confidence interval.
Note that the only case where the DL model does not rank first is when diagnosing female patients using hand X-rays, where it comes second after BaseDT. It is shown in the complementary material that the extra covariate data contributed to better performance and removing those causes the BaseDT to perform worse.
The pelvis model had the best classification performance, which may be due to the fact that the pelvis X-rays the femoral neck, which will have a substantial contribution to the BMD estimate of the femoral neck, whereas the knee and hand X-rays do not.
Discussion
Key findings
This study showcases the potential of modern machine learning in identifying patients with low BMD from routinely acquired X-rays, even when the femoral neck is not included in the field of view. By comparing to baseline models, this study demonstrates that imaging data contains rich diagnostic information that can be extracted with modern machine learning approaches. A radiologist can detect osteopenia on conventional radiographs only when 20–40% of bone mass has been lost (24). As an example, if someone had a BMD of 0.858 g/cm2 at the femoral neck [which is the mean BMD for a female aged 20–29 years from NHANES III (18)], then a loss of 30% of bone mass would correspond to a T-score of −2.1 [assuming the use of a female reference population as recommended by WHO (23)]. Similarly, if someone had a BMD of 1.064 g/cm2 at L1–L4 [which is the mean BMD for a female aged 20–29 years from NHANES (25)], then a loss of 30% would correspond to a T-score of −3.0. As such, an algorithm that can identify the earlier stage of demineralization, at a T-score of −1, offers an advantage to the human eye.
Strengths and limitations
Strengths of the current method and study include the performance of the algorithm without the need for segmentation or manual feature extraction, and its ability to estimate BMD at the femoral neck, even when the femoral neck is not in the X-ray analyzed (i.e., in X-rays of the knee and hand). This study had several limitations. First, the dataset included only patients with OA, which could limit generalizability of the algorithms to patients without OA. Second, although the dataset was created from multiple centers, all the centers were in the United States. Third, only GE Lunar machines were used to determine the DXA-derived BMD, as such, claims cannot be made in predicting BMD derived from other DXA machines, although there are clinically accepted ways to convert BMD units across machines and T-scores also serve as a common unit. Finally, the study was a relatively small dataset which is known to be the ‘Achilles heel’ of DL approaches. Although small, this study employed commonly applied data augmentation strategies and relied on the assumption that BMD is relatively stable over a 24-month period (t) in order to increase the number of labeled samples available for training.
Comparison with similar research
A number of approaches to screen for osteoporosis from conventional X-rays have been proposed. The majority of these have used pelvic (11,12) or lumbar (14) X-rays, and have shown utility in predicting BMD of those body parts, given that osteoporosis is monitored at those sites. Other researchers have had success predicting BMD from chest X-rays (13). A large study recently extended the utility of a deep-learning algorithm to include fracture risk assessment (12). The current study shows similar results when estimating femoral neck BMD from the pelvic X-rays, but also estimates femoral neck BMD and T-score from X-rays of body parts that do not include the femur, namely the hand and knee. Fewer studies have estimated BMD from hand X-rays. Tecle et al. (10) trained a CNN to detect osteoporosis from hand radiographs which achieved a sensitivity and specificity of 82% and 95%, respectively, for classifying low BMD vs. normal BMD. The main difference between this method and ours is that it did not train using low BMD by DXA as the ground truth, rather it used second metacarpal cortical percentage (MCP) as an osteoporosis predictor (26). In another related work (27), the authors introduce a tool to detect and segment areas with low bone mass on hand and wrist radiographs using cortical radiogrammetry of third metacarpal bone and trabecular texture analysis of distal radius. This tool used engineered features and achieved lower classification accuracy as the DL model presented in this study.
Explanations of findings
The DL model showed more narrow limits of agreement with ground truth BMD by DXA than the alternative models. The AUC of the model was >0.80 for detecting low BMD from X-rays of the hand (0.85 in females, 0.82 in males), knee (0.87 in females, 0.89 in males), and pelvis (0.92 in females, 0.88 in males), demonstrating the discriminating power of the model to identify patients with low BMD (T-score <−1).
Implications and actions needed
Routine X-rays are by far the most performed medical imaging test. Incorporation of a DL modeling to opportunistically analyze X-rays could serve to screen the population for patients who would benefit from formal diagnosis with DXA. While the DL model will be unlikely to rival the accuracy and precision of DXA in the quantification of low BMD, an opportunistic screening approach is particularly attractive because it can help identify and prioritize patients who are currently overlooked. Osteoporosis has a known care gap (5). It is prevalent, silent, and preventable with treatment. Radiologists can include a finding of suspected low BMD in their X-ray report to encourage referring physicians to conduct a clinical fracture risk assessment and refer their patient for DXA if appropriate.
Conclusions
These results indicate that low BMD at the femoral neck can be opportunistically screened from routinely acquired X-rays of the hand, knee, or pelvis, i.e., even when the femoral neck is not included in the field of view. Early identification of patients with low BMD is of tremendous value to both the patients’ wellbeing and to the healthcare system when considering the significant downstream costs associated with osteoporotic fractures.
Acknowledgments
Data used in the preparation of this manuscript were obtained and analyzed from the controlled access datasets distributed from the Osteoarthritis Initiative (OAI), a data repository housed within the NIMH Data Archive (NDA). OAI is a collaborative informatics system created by the National Institute of Mental Health and the National Institute of Arthritis, Musculoskeletal and Skin Diseases (NIAMS) to provide a worldwide resource to quicken the pace of biomarker identification, scientific investigation, and OA drug development. Dataset identifier(s): 10.15154/1519166.
Funding: This work was supported by
Footnote
Peer Review File: Available at https://jmai.amegroups.com/article/view/10.21037/jmai-23-10/prf
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jmai.amegroups.com/article/view/10.21037/jmai-23-10/coif). CAS is Head of Research & Quality at 16 Bit. AB is on the scientific advisory board of Osteoporosis Canada. He holds stock in a company he co-founded called 16 Bit which manufactures a Health Canada approved medical device which operates in the osteoporosis space. He is an inventor on a patent that is related to measuring BMD from routine X-rays. 16 Bit has received funding from Amgen Canada and INOVAIT to support product development. MDC is the Co-Founder and Co-CEO of 16 Bit which supported this research project with assistance from Amgen Canada. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The OAI was conducted in accordance with the Declaration of Helsinki defined in the 1964 and meets all amendments made after. OAI was approved by each site’s IRB: Memorial Hospital of Rhode Island (Pawtucket, RI, USA) Ohio State University (Columbus, OH, USA), University of Pittsburgh (Pittsburgh, PA, USA), and University of Maryland/Johns Hopkins University (Baltimore, MD, USA) and at the coordinating center (University of California, San Francisco, CA, USA; approval number 10-00532). All participants provided informed consent prior to participation.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Kanis JA. Assessment of osteoporosis at the primary health-care level. Technical Report. 2007. Available online: https://frax.shef.ac.uk/FRAX/pdfs/WHO_Technical_Report.pdf
- Wright NC, Looker AC, Saag KG, et al. The recent prevalence of osteoporosis and low bone mass in the United States based on bone mineral density at the femoral neck or lumbar spine. J Bone Miner Res 2014;29:2520-6. [Crossref] [PubMed]
- Johnell O, Kanis J. Epidemiology of osteoporotic fractures. Osteoporos Int 2005;16:S3-7. [Crossref] [PubMed]
- Moran CG, Wenn RT, Sikand M, et al. Early mortality after hip fracture: is delay before surgery important? J Bone Joint Surg Am 2005;87:483-9. [PubMed]
- Miller PD. Underdiagnosis and Undertreatment of Osteoporosis: The Battle to Be Won. J Clin Endocrinol Metab 2016;101:852-9. [Crossref] [PubMed]
- Black DM, Rosen CJ. Postmenopausal Osteoporosis. N Engl J Med 2016;374:2096-7. [Crossref] [PubMed]
- US Preventive Services Task Force. Screening for Osteoporosis to Prevent Fractures: US Preventive Services Task Force Recommendation Statement. JAMA 2018;319:2521-31. [Crossref] [PubMed]
- Gillespie CW, Morin PE. Trends and Disparities in Osteoporosis Screening Among Women in the United States, 2008-2014. Am J Med 2017;130:306-16. [Crossref] [PubMed]
- Alswat KA. Gender Disparities in Osteoporosis. J Clin Med Res 2017;9:382-7. [Crossref] [PubMed]
- Tecle N, Teitel J, Morris MR, et al. Convolutional Neural Network for Second Metacarpal Radiographic Osteoporosis Screening. J Hand Surg Am 2020;45:175-81. [Crossref] [PubMed]
- Ho CS, Chen YP, Fan TY, et al. Application of deep learning neural network in predicting bone mineral density from plain X-ray radiography. Arch Osteoporos 2021;16:153. [Crossref] [PubMed]
- Hsieh CI, Zheng K, Lin C, et al. Automated bone mineral density prediction and fracture risk assessment using plain radiographs via deep learning. Nat Commun 2021;12:5472. [Crossref] [PubMed]
- Sato Y, Yamamoto N, Inagaki N, et al. Deep Learning for Bone Mineral Density and T-Score Prediction from Chest X-rays: A Multicenter Study. Biomedicines 2022;10:2323. [Crossref] [PubMed]
- Zhang B, Yu K, Ning Z, et al. Deep learning of lumbar spine X-ray for osteopenia and osteoporosis screening: A multicenter retrospective cohort study. Bone 2020;140:115561. [Crossref] [PubMed]
- Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing Systems 2012;25:1097-105.
- Peterfy CG, Schneider E, Nevitt M. The Osteoarthritis Initiative: report on the design rationale for the magnetic resonance imaging protocol for the knee. Osteoarthritis Cartilage 2008;16:1433-41. [Crossref] [PubMed]
- Archive NIMHD. The Osteoarthritis Initiative (OAI) Dataset. Available online: https://www.niams.nih.gov/grants-funding/funded-research/osteoarthritis-initiative
- Looker AC, Orwoll ES, Johnston CC Jr, et al. Prevalence of low femoral bone density in older U.S. adults from NHANES III. J Bone Miner Res 1997;12:1761-8. [Crossref] [PubMed]
- Carstensen B. Comparing methods of measurement: Extending the LoA by regression. Stat Med 2010;29:401-10. [Crossref] [PubMed]
- Passing H. Bablok. A new biometrical procedure for testing the equality of measurements from two different analytical methods. Application of linear regression procedures for method comparison studies in clinical chemistry, Part I. J Clin Chem Clin Biochem 1983;21:709-20. [PubMed]
- Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307-10. [Crossref] [PubMed]
- cutpointr: Determine and Evaluate Optimal Cutpoints in Binary Classification Tasks. 2021. Available online: https://cran.r-project.org/web/packages/cutpointr/cutpointr.pdf
-
Official Positions Adult ISCD - Brunader R, Shelton DK. Radiologic bone assessment in the evaluation of osteoporosis. Am Fam Physician 2002;65:1357-64. [PubMed]
- Looker AC, Borrud LG, Hughes JP, et al. Lumbar spine and proximal femur bone mineral density, bone mineral content, and bone area: United States, 2005-2008. Vital Health Stat 11 2012;1-132. [PubMed]
- Schreiber JJ, Kamal RN, Yao J. Simple Assessment of Global Bone Density and Osteoporosis Screening Using Standard Radiographs of the Hand. J Hand Surg Am 2017;42:244-9. [Crossref] [PubMed]
- Areeckal AS, Kamath J, Zawadynski S, et al. Combined radiogrammetry and texture analysis for early diagnosis of osteoporosis using Indian and Swiss data. Comput Med Imaging Graph 2018;68:25-39. [Crossref] [PubMed]
Cite this article as: Golestan K, Syme CA, Bilbily A, Zuberi S, Volkovs M, Poutanen T, Cicero MD. Approximating femoral neck bone mineral density from hand, knee, and pelvis X-rays using deep learning. J Med Artif Intell 2023;6:7.


