
Machine learning versus logistic regression for permanent pacemaker implantation prediction after transcatheter aortic valve replacement—a systematic review and meta-analysis
Highlight box
Key findings
• Our study reports that machine learning (ML) algorithms do not perform significantly better than logistic regression (LR) models in predicting permanent pacemaker implantation after transcatheter aortic valve replacement.
What is known and what is new?
• ML algorithms have yielded conflicting results as prediction models but hold promise as the full extent of their potential remains largely unexplored and it is a rapidly evolving field with frequent unforeseen new applications.
What is the implication, and what should change now?
• Enhancing and gaining a deeper understanding of existing ML models, then subjecting them to rigorous testing on a sizable patient cohort, could demonstrate their superiority over traditional LR models.
Introduction
Transcatheter aortic valve replacement (TAVR) has improved the clinical management of aortic valve disease in recent years (1,2). TAVR was initially performed in patients with symptomatic aortic valve stenosis deemed high-risk for cardiac surgery (2). Successively, TAVR evolved into an established therapeutic option for lower-risk cardiac surgery patients as well, given the non-inferiority in terms of mortality and post-operative complications to surgical aortic valve replacement (SAVR) (3,4). However, compared with SAVR, TAVR is associated with a higher incidence of major vascular complications, paravalvular regurgitation, aortic-valve reintervention, and pacemaker implantations (2-4).
Despite improved procedural techniques and newer-generation valves, the main complication of TAVR remains the development of conduction abnormalities, often leading to permanent pacemaker implantation (PPI) (5,6). Notably, the rate of PPI in TAVR is two to five times higher than that of SAVR (7,8). Post-TAVR conduction disturbances substantially impact the patients’ quality of life. An accurate prediction for post-TAVR PPI has become fundamental for clinical decision-making. Anticipating the need for PPI prior to TAVR could allow patients, with the guide of the cardiac team, to take an informed decision based on concrete data.
Specific baseline characteristics, such as age, sex, and pre-existing heart-rhythm abnormalities have already been identified as factors associated with PPI (9,10). Based on these characteristics, several models have been developed. Logistic regression (LR) has been the gold standard statistical tool in pacemaker implantation prediction after TAVR (11,12).
Nowadays, artificial intelligence (AI) has demonstrated promising results in prediction of clinical outcomes, and its role is rapidly expanding in cardiac surgery (13-15). AI encompasses analytical algorithms that iteratively learn from data. Machine learning (ML) is a subset of AI that develops algorithms enabling computers to learn and make predictions based on data, progressively enhancing performance through experience and repetition (16). Within the subset of ML, random forest (RF) stands as a versatile algorithm that combines individual model predictions, creating a more accurate prediction model. RF has been one of the most applied ML algorithms in the past decade in the medical field (17,18). In fact, it excels in both classification and regression tasks, making it ideal for constructing precise clinical prognostic models. However, despite its potential applications, prior analyses have demonstrated contradictory results regarding RF, and in general, AI discrimination ability in the clinical setting (19,20).
We have conducted a study-level meta-analysis which compares ML models with LR models to predict the association between peri-procedural risk factors and PPI in patients who underwent TAVR. We present this article in accordance with the PRISMA reporting checklist (available at https://jmai.amegroups.com/article/view/10.21037/jmai-23-162/rc).
Methods
Institutional Review Board approval of this analysis was not required as no human or animal subjects were involved. The present review was registered with the National Institute for Health Research International Registry of Systematic Reviews (PROSPERO, CRD42023467471). The manuscript follows the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines (Figure 1).
Search strategy
A medical librarian (M.D.) performed a comprehensive literature search to identify articles comparing ML and LR prediction models for PPI in patients post-TAVR. Searches were performed in August 2023 and included three databases: Ovid MEDLINE (All; 1946 to present), Ovid EMBASE (1974 to present) and Cochrane Library. The complete search strategy is available in Table S1.
Study selection and data extraction
After de-duplication, studies were screened by two independent reviewers (M.D.A. and T.C.) and discrepancies were resolved by the senior author (M.G.). A first round of screening based on title and abstract content was performed and studies were considered for inclusion if they were written in English and compared ML and LR prediction models for PPI in patients after TAVR. Animal studies, abstracts, case reports, commentaries, editorials, expert opinions, conference presentations, studies with pediatric populations, and studies not reporting the outcomes of interest were excluded. The full text was pulled for the selected studies for a second round of eligibility screening. References for articles selected were also reviewed for relevant studies not captured by the original search.
Three investigators (M.D.A., C.S.R. and T.C.) independently performed data extraction and the integrity was verified by the corresponding author (M.G.). The extracted variables included study characteristics (publication year, country, sample size, study design, follow-up and population adjustments) as well as patient demographics [age, sex, body mass index (BMI), diabetes, smoking status, hypertension, coronary artery disease (CAD), peripheral vascular disease (PVD), previous cardiac surgery and previous cardiovascular accident (CVA)], baseline transthoracic echocardiogram (TTE) characteristics [left ventricular ejection fraction (LVEF), aortic valve area (AVA), mean aortic value pressure gradient (AVPG), size of left ventricular outflow tract (LVOT)], pre-procedural ECG findings [right bundle branch block (RBBB), left bundle branch block (LBBB), atrioventricular block (AVB), PR interval, QRS interval], Society of Thoracic Surgeon (STS) score and valve characteristics (balloon-expandable, self-expandable, mechanically expandable, valve size) (Table S2). Furthermore, all available models’ data were extracted [accuracy, precision, F1 score, Brier score, area under the curve (AUC), true positive (TP), false positive (FP)], according to the CHARMS checklist (21) and the QUADAS risk of bias tool (22).
The quality of the included studies was assessed using the Newcastle-Ottawa risk of bias assessment scale (23) (Table S3) and the risk of bias assessment model as proposed by Christodoulou and colleagues (19) (Table S4).
Outcomes
The primary outcome was PPI prediction post-TAVR (defined as permanent implantation of an adjustable artificial electrical pulse generator) comparing ML and LR models’ predictive power. Included articles’ outcomes were reported in Table S5. Significant predictive variables used for models’ construction were reported in Table S6. Only the RF-based models were considered for analysis and compared to LR models, being the algorithm reported by the three articles included.
Statistical analysis
Model performance was primarily assessed in terms of discrimination ability for PPI prediction. Discrimination refers to a prediction model’s ability to distinguish between subjects developing and not developing the outcome and is quantified by the concordance (C)-statistic, that corresponds to the AUC. The C-statistic is an estimated conditional probability that for any pair of a subject who experienced and a subject who did not experience the outcome, the predicted risk of an event is higher for the former.
After all relevant studies were identified and results were extracted from them, the retrieved estimates of C-statistic for ML and LR models were summarized into a weighted average to provide an overall summary of their performance. Moreover, the overall accuracy was presented as net benefit.
A Bayesian estimation framework was utilized to calculate the meta-analytic estimates. For our main analysis, ML and LR models were extracted and pooled from each study. Pooled C-statistics (PCS) for ML models and LR were then compared using the method described by Hanley et al. (24).
As a sensitivity analysis, the main comparison was performed excluding derivation models and models with extremely reduced accuracy levels. The presence of small-study effects was checked by visual inspection of the funnel plot and tested by fitting a regression directly to the data using the treatment effect as the dependent variable, and standard error as the independent variable for ML models performance.
Bayesian methods utilize formal probability models to express uncertainty about parameter values. Bayesian inference consists of repeatedly sampling from a posterior distribution in order to get parameter estimates and their variance. Just Another Gibbs Sampler (JAGS) and Markov Chain Monte Carlo (MCMC) Simulation were used for sampling. The convergence of all estimated Bayesian meta-analysis models was verified by calculating the potential scale reduction factor of the Gelman-Rubin statistic autocorrelation of the sample (>1.05 indicative of non-convergence). PCS and 95% credibility interval (CI) were directly obtained from the corresponding posterior quantiles for ML and LR models from the same sample. Depiction of the extent of between-study heterogeneity was shown by calculation of 95% prediction interval.
All analyses were performed using R version 4.3.1 and metamisc and rjags packages. All statistical tests were 2-sided.
Results
Meta-analytic data
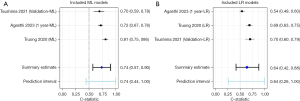
In this meta-analysis, we included 2,681 patients from three studies. No significative difference was noticed in the predictive accuracy between ML and LR models [ML PCS (95% CI): 0.72 (0.63–0.81) vs. LR PCS (95% CI): 0.64 (0.50–0.78) net benefit (%) +8.0; P=0.34] (Figure 2, Tables 1,2). Excluding the derivation model from Tsushima and 1 year model from Agasthi showed no significant difference [ML PCS (95% CI): 0.72 (0.51–0.92) vs. LR PCS (95% CI): 0.64 (0.43–0.88); net benefit (%) +8.0; P=0.60] (Figure 3, Table 2).

Table 1
| Author | Year of publication | Country | No. of patients | Study design | Mean follow-up | Extracted outcomes | ||
|---|---|---|---|---|---|---|---|---|
| Model: total patients | No-PPI | PPI | ||||||
| Agasthi et al. (26) | 2023 | USA | 30-day: 964 | 775 | 189 | Retrospective cohort study | 30-day, 1-year | PPI AUC |
| 1-year: 657 | 481 | 176 | ||||||
| Tsushima et al. (20) | 2021 | USA | Derivation: 888 | 704 | 184 | Retrospective cohort study | Perioperative | PPI AUC |
| Validation: 272 | 234 | 38 | ||||||
| Truong et al. (25) | 2020 | USA | 557 | 462 | 95 | Retrospective cohort study | Perioperative | PPI AUC |
PPI, permanent pacemaker implantation; AUC, area under the curve.
Table 2
| Variable | Models considered (N) | 95% credibility interval | Net benefit (%) | P value | |
|---|---|---|---|---|---|
| ML pooled C-statistic | LR pooled C-statistic | ||||
| All | 5 | 0.72 (0.63–0.81) | 0.64 (0.50–0.78) | +8.0 | 0.34 |
| Excluding Tsushima derivation model and Agasthi 1 year model | 3 | 0.72 (0.51–0.92) | 0.64 (0.43–0.88) | +8.0 | 0.60 |
| Excluding Tsushima derivation model and Agasthi 30 days model | 3 | 0.74 (0.57–0.90) | 0.64 (0.42–0.88) | +10.0 | 0.28 |
ML, machine learning; LR, logistic regression.

Excluding the derivation model from Tsushima and the 30 days model from Agasthi showed no statistical significance in discriminatory power [ML PCS (95% CI): 0.74 (0.57–0.90) vs. LR PCS (95% CI): 0.64 (0.42–0.88) net benefit (%) +10.0; P=0.28] (Figure 4, Table 2).
Funnel plot and regression test showed no evidence of small study effect (P=0.79) (Figure S1).
From the box plot it is evident that ML models have a smaller distribution compared to LR prediction models, but given the right-skewed median line, no significant difference can be inferred (Figure S2).
Analysis of the individual studies
Truong et al. RF model
The ML model created by Truong et al. (25) using RF methodology demonstrated the highest discriminatory power in PPI and improved accuracy compared to traditional LR model (RF AUC 0.81; 95% CI: 0.75–0.86; accuracy 0.76; F1 score 0.49; Brier score 0.18; versus LR AUC 0.69; 95% CI: 0.63–0.75; accuracy 0.68; F1 score 0.41; Brier score 0.23) (Figure 2, Tables 1,2).
The RF and LR models were created using a training set (75%) and a validation set (25%). RF outperformed the other ML models created by the authors in post-TAVR PPI prediction (classical decision tree AUC 0.64; conditional inference trees AUC 0.70; support vector machine AUC 0.67; extreme gradient boost AUC 0.73; neural network AUC 0.70).
Among 557 total patients, PPI occurred in 95 patients (17.1%). Indications for PPI were complete AVB (75%), pathological pauses and asystole (6%) and other conditions (Mobitz type II AV block, high grade AV block, symptomatic junctional rhythm, symptomatic bradycardia, and symptomatic prolonged PR interval) (19%).
On electrocardiogram (ECG) at baseline, patients who underwent PPI after TAVR had longer PR intervals (P=0.005), wider QRS interval (≥120 ms) (P<0.001), RBBB (P<0.001) and first-degree AV block (P<0.001). On post-operative ECG, delta PR and delta QRS predicted PPI more accurately than baseline characteristics (P<0.001). The RF model including post-TAVR ECG outperformed the models without post-TAVR data. Delta QRS (P<0.001), delta PR (P<0.001), baseline QRS interval (P<0.001), baseline RBBB (P<0.001), baseline PR interval (P<0.001) were the variables associated with PPI post-TAVR.
Agasthi et al. RF-GBM model
The ML model created by Agashti et al. (26) using RF gradient boosting machine (GBM) methodology outperformed the LR for PPI post-TAVR. Whereas RF algorithms built an ensemble of deep independent trees for prediction, RF-GBMs build an ensemble of shallow and weak successive trees with each tree learning and improving on the previous. At 1 year, the GBM model had a higher discriminatory power compared to the LR PPI risk score (RF-GBM AUC, 0.72; 95% CI: 0.67–0.76 vs. LR AUC, 0.54; 95% CI: 0.49–0.60; P<0.001) (Figure 2, Tables 1,2). At 30 days, both GBM and LR models’ predictive power decreased (RF-GBM AUC 0.66; 95% CI: 0.61–0.70 vs. LR AUC 0.55; 95% CI: 0.49–0.60; P<0.001) (Figure 2, Tables 1,2). Due to a small percentage of events the authors did not divide the dataset in derivation and validation cohorts. A 5-fold cross-validation was repeated 10 times.
Among the 964 patients analyzed in the 30 days analysis, 19.6% (n=189) needed a PPI after undergoing TAVR. In the 1 year analysis involving 657 patients, 26.7% (n=176) required a PPI after TAVR. In the 30 days analysis, the most influential baseline predictors were the presence of RBBB (P<0.001), a higher pre-operative risk (P<0.001), the use of self-expanding valves (P<0.001) an increased QRS interval (P<0.001). In the 1 year analysis, the most influential baseline predictors were a greater ratio of the brachiocephalic artery to the aortic valve annulus relative to patient height (P<0.001), a higher mean gradient across the mitral valve during diastole (P<0.001), the presence of RBBB (P<0.001), a larger LVOT diameter (P<0.001), a greater distance between the right coronary artery and the basal ring (P<0.001) and increased QRS interval (P<0.001).
Tsushima et al. RF model
Tsushima et al. (20) found that RF did not outperform the LR model in PPI post-TAVR (AUC RF, 0.70; 95% CI: 0.59–0.78; precision 0.77; F-Measure 0.50; MCC 0.30; vs. AUC LR, 0.70; 95% CI: 0.60–0.79; precision 0.62; F-Measure 0.61; MCC 0.23) (Figure 2, Tables 1,2).
The authors compared different ML algorithms [IBk, Random Tree, Multilayer Perceptron, RF, REP tree, J48, JRip, Naïve Bayes, Bayesian network, decision table, sequential minimal optimization (SMO), locally weighted learning (LWL)] and two types of LR [logistic regression and simple logistic regression (SLR)] (Table S7). In order to be coherent with the other articles and models analyzed, we considered RF and normal LR for analysis. Even considering the best performing ML model (LWL) and SLR, no significant difference was noted between the models in terms of discrimination power. Eight hundred and eighty-eight patients were included in group A (derivation), and 272 patients were in group B (validation). RF models’ derivation was performed with a ten-fold cross validation. In the derivation group, 184 patients (20.7%) required new PPI, and the major indications were complete heart block (70.1%) and new left bundle branch block with subsequent high-grade AVB in 23.4%. In the validation group, 38 patients (14.0%) required PPI similarly for complete heart block in 71.1% and new left bundle branch block in 26.3%, respectively. At baseline, variables which influenced successive PPI in the derivation group were hypertension (P=0.005), LBBB (P=0.003), RBBB (P<0.001), AVB (P=0.005), QRS interval (P<0.001), and self-expanding valves (P<0.001). In the validation group, baseline characteristics which predicted PPI were RBBB (P<0.001) and QRS interval (P<0.001).
Discussion
Based on our analysis, ML models do not show significantly better discrimination ability than LR models (Table 1).
Although the analysis yielded non-significant results, the PCS estimates of ML models result in a net benefit of 8.0% compared to that of LR models (Figure 2, Table 2). We could not demonstrate an improved discriminatory capacity from a different ML model than RF.
The quality of life for patients is significantly affected by conduction disturbances post-TAVR. Anticipating the requirement for PPI would enable patients to explore alternative treatment options like SAVR. There is a rising interest in the development of risk-prediction models for clinical use to facilitate multidisciplinary shared decision-making. In the pursuit of heightened precision and accuracy, there is an increasing application of AI for clinical risk predictions.
However, no comparison existed between ML and LR prediction models for PPI following TAVR.
LR models have been used to predict PPI after TAVR. However, LR models need the user’s involvement to manipulate intricate interactions among features. The potential advantage that ML models hold over traditional LR is the ability of capturing nonlinearity and feature interactions without requiring direct user’s involvement. Furthermore, in contrast to LR, ML demonstrates more effective handling of missing data by forgoing reliance on data distribution assumptions and engaging in complex calculations.
ML based models prove to be effective for predictive modeling. Specifically, RF models reduce the high variance present in a flexible model by combining numerous decision trees into a single model. Furthermore, RF models result the most suitable approach when it is essential to understand the variables influencing the prediction.
Nevertheless, the results obtained do not support the hypothesis that ML models can achieve superior discrimination compared to LR models, improving prediction of PPI after TAVR. According to our results, unless substantiated by extensive data quantities, the advantage of ML is not significantly superior to LR.
The non-significance of ML PCS can be attributed to several factors.
As ML models require a large amount of data, our analysis was influenced by the paucity of articles comparing ML and LR models having PPI as endpoint and their reduced samples size. In a meta-analysis with a larger sample of patients, Benedetto et al. demonstrated that ML models exhibit superior discriminatory capacity in predicting mortality following cardiac surgery with a 7.0% net benefit (ML, 0.88; 95% CI: 0.83–0.93 vs. LR, 0.81; 95% CI: 0.77–0.85; P=0.03) (15). Thus, studies with larger cohorts could statistically confirm our findings.
Larger data sample is not the sole factor to consider. Testing various ML models is essential since there is no single model that universally performs best for every cohort or dataset, a concept encapsulated by the No Free-Lunch theorem (23). The assumptions that make a model effective for one dataset may not hold true for another, prompting the experimentation of multiple ML models to identify the most suitable one for a specific dataset. In addition, ML algorithms introduce learning bias, assumptions about the relationships between predictors and outcomes. Based on these assumptions, certain algorithms may fit specific datasets more effectively than others.
In our study, we focused on RF models, as it was the algorithm reported in all three considered articles. However, the authors tested several ML algorithms on the same patient cohort in order to determine which model would be the most apt for PPI prediction after TAVR. Tsushima et al. and Truong et al. demonstrated the discriminatory ability among different algorithms on the same cohort (20,25). To ascertain the most suitable model for predicting PPI after TAVR, additional studies incorporating diverse algorithms across various cohorts are fundamental.
Furthermore, all three articles considered present absence of details regarding both the execution and outcomes for ML and LR models (Table S8). The authors do not indicate learning methods, software use, tuning, calibration and degree of supervision for the ML models. For LR models there is no indication of whether appropriate linearizing transformations of scale were applied or if interaction terms were considered. This hints potential misspecification in the models.
Truong et al. are the only authors to address validation and data imbalance. Truong and colleagues employ Synthetic Minority Oversampling Technique (SMOTE), a technique that balances the occurrence of events and no events, generating synthetic minority class observations. Additionally, the authors consider both pre-procedural and early post-procedural variables for their models. Considering that clinically, PPI typically occurs several days postoperative, the inclusion of early post-procedural variables represents a sensible decision clinically.
Agasthi et al. apply a RF-GBM algorithm, without further specifications. Both algorithms are ensemble learning methods and make a prediction by combining the outputs from individual trees. Gradient boosting decision trees (GBT) build trees one at a time, where each new tree helps to correct errors made by previously trained tree. RFs train each tree independently, using a random sample of the data. However, it is difficult to understand how the two methods were applied in order to build the model.
Another fundamental point is represented by clinical relevance. Models must align with clinical practicality and versatility. The application of ML models for patient risk prediction should be both intuitive and expeditious. The models’ adaptability should extend across diverse populations, it should be scalable, and it should learn from novel data input. Additionally, integration with the patient’s electronic records would ensure privacy adherence. While achieving a perfect prediction accuracy remains challenging, a model with these functionalities would significantly benefit both patients and physicians in their decision-making processes.
Taken together, the introduction of ML in clinical outcomes prediction shows potential, but its effectiveness is contingent on large data samples, dataset suitability, model and methodology quality and clinical relevance. Our results suggest that the impact of ML on PPI prediction after TAVR remains uncertain. ML and LR models may not perform significantly different when developed using small datasets. Addressing current limitations in ML modelling could pave the way for improvements in clinical risk prediction, potentially surpassing LR in the near future.
Limitations
Limitations were identified in our study. First and foremost, the scarcity of data on PPI after TAVR poses a significant constraint, limiting the statistical significance and thus, the generalizability of the results obtained. The presence of purely RF-based models in two of the three studies included, further narrows the scope, omitting potential insights from other ML algorithms. The individual studies’ decision to exclude prediction of other endpoints (e.g., survival) and to focus exclusively on PPI prediction may overlook clinically relevant post-TAVR aspects.
The included studies are single-center retrospective studies, whose prediction models derive from older cohorts. This temporal gap may compromise the relevance of incidence rates of PPI post-TAVR due to the development of better TAVR procedures and the increased scrutiny of postoperative complications in recent years.
The considered models’ predictive ability relies on slightly different predictive variables, despite all employing the same outcome measure.
Besides modelling, PPI post-TAVR does not have an exact definition in scientific literature, and no specific timeframe has yet been established. Agreeing on a determined definition of PPI after TAVR is necessary as it could impact the predictive power of any model. In our study, excluding the 30 days model of Agasthi from the analysis led to an increased Net benefit (Table 2).
Agasthi et al. was the only study to include important variables, such as the type of valve and preoperative health conditions. This discrepancy in variable selection could impact the comparability and completeness of the predictive models. Lastly, Agasthi et al. use a RF-GBM algorithm. This algorithm, despite based on the same concept, is not equivalent to RF algorithm, potentially influencing the results and final analysis.
These limitations collectively underscore the need for cautious interpretation and highlight avenues for future research to address these constraints and enhance the robustness of predictive modeling in the context of PPM post TAVR.
Conclusions
Despite showing a higher net benefit, ML models do not perform significantly better than LR models in predicting the association between peri-procedural risk factors and PPI after TAVR.
Acknowledgments
Funding: None.
Footnote
Reporting Checklist: The authors have completed the PRISMA reporting checklist. Available at https://jmai.amegroups.com/article/view/10.21037/jmai-23-162/rc
Data Sharing Statement: Available at https://jmai.amegroups.com/article/view/10.21037/jmai-23-162/dss
Peer Review File: Available at https://jmai.amegroups.com/article/view/10.21037/jmai-23-162/prf
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jmai.amegroups.com/article/view/10.21037/jmai-23-162/coif). T.C. was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Clinician Scientist Program OrganAge funding number 413668513, by the Deutsche Herzstiftung (DHS, German Heart Foundation) funding number S/03/23 and by the Interdisciplinary Center of Clinical Research of the Medical Faculty Jena. L.H. is partially supported by a T-32 training grant in cardiovascular disease from the National Heart, Lung, and Blood Institute (1 T32 HL160520-01A1). M.G. received research grants from the National Institutes of Health, the Canadian Health and Research Institutes and the Starr Foundation. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. IRB approval and informed consent are waived as no human subject is involved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Avvedimento M, Tang GHL. Transcatheter aortic valve replacement (TAVR): Recent updates. Prog Cardiovasc Dis 2021;69:73-83. [Crossref] [PubMed]
- Cahill TJ, Terre JA, George I. Over 15 years: the advancement of transcatheter aortic valve replacement. Ann Cardiothorac Surg 2020;9:442-51. [Crossref] [PubMed]
- Makkar RR, Thourani VH, Mack MJ, et al. Five-Year Outcomes of Transcatheter or Surgical Aortic-Valve Replacement. N Engl J Med 2020;382:799-809. [Crossref] [PubMed]
- Zhao PY, Wang YH, Liu RS, et al. The noninferiority of transcatheter aortic valve implantation compared to surgical aortic valve replacement for severe aortic disease: Evidence based on 16 randomized controlled trials. Medicine (Baltimore) 2021;100:e26556. [Crossref] [PubMed]
- Auffret V, Puri R, Urena M, et al. Conduction Disturbances After Transcatheter Aortic Valve Replacement: Current Status and Future Perspectives. Circulation 2017;136:1049-69. [Crossref] [PubMed]
- Karyofillis P, Kostopoulou A, Thomopoulou S, et al. Conduction abnormalities after transcatheter aortic valve implantation. J Geriatr Cardiol 2018;15:105-12. [PubMed]
- Cao C, Ang SC, Indraratna P, et al. Systematic review and meta-analysis of transcatheter aortic valve implantation versus surgical aortic valve replacement for severe aortic stenosis. Ann Cardiothorac Surg 2013;2:10-23. [PubMed]
- Hamm CW, Möllmann H, Holzhey D, et al. The German Aortic Valve Registry (GARY): in-hospital outcome. Eur Heart J 2014;35:1588-98. [Crossref] [PubMed]
- Siontis GC, Jüni P, Pilgrim T, et al. Predictors of permanent pacemaker implantation in patients with severe aortic stenosis undergoing TAVR: a meta-analysis. J Am Coll Cardiol 2014;64:129-40. [Crossref] [PubMed]
- Schroeter T, Linke A, Haensig M, et al. Predictors of permanent pacemaker implantation after Medtronic CoreValve bioprosthesis implantation. Europace 2012;14:1759-63. [Crossref] [PubMed]
- Maeno Y, Abramowitz Y, Kawamori H, et al. A Highly Predictive Risk Model for Pacemaker Implantation After TAVR. JACC Cardiovasc Imaging 2017;10:1139-47. [Crossref] [PubMed]
- Vejpongsa P, Zhang X, Bhise V, et al. Risk Prediction Model for Permanent Pacemaker Implantation after Transcatheter Aortic Valve Replacement. Struct Heart 2018;2:328-35. [Crossref]
- Dias RD, Shah JA, Zenati MA. Artificial intelligence in cardiothoracic surgery. Minerva Cardioangiol 2020;68:532-8. [Crossref] [PubMed]
- Mumtaz H, Saqib M, Ansar F, et al. The future of Cardiothoracic surgery in Artificial intelligence. Ann Med Surg (Lond) 2022;80:104251. [Crossref] [PubMed]
- Benedetto U, Dimagli A, Sinha S, et al. Machine learning improves mortality risk prediction after cardiac surgery: Systematic review and meta-analysis. J Thorac Cardiovasc Surg 2022;163:2075-2087.e9. [Crossref] [PubMed]
- Rowe M. An Introduction to Machine Learning for Clinicians. Acad Med 2019;94:1433-6. [Crossref] [PubMed]
- Alam MdZ. Rahman MS, Rahman MS. A Random Forest based predictor for medical data classification using feature ranking. Inform Med Unlocked 2019;15:100180. [Crossref]
- Banerjee M, Reynolds E, Andersson HB, et al. Tree-Based Analysis. Circ Cardiovasc Qual Outcomes 2019;12:e004879. [Crossref] [PubMed]
- Christodoulou E, Ma J, Collins GS, et al. A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. J Clin Epidemiol 2019;110:12-22. [Crossref] [PubMed]
- Tsushima T, Al-Kindi S, Nadeem F, et al. Machine Learning Algorithms for Prediction of Permanent Pacemaker Implantation After Transcatheter Aortic Valve Replacement. Circ Arrhythm Electrophysiol 2021;14:e008941. [Crossref] [PubMed]
- Moons KG, de Groot JA, Bouwmeester W, et al. Critical appraisal and data extraction for systematic reviews of prediction modelling studies: the CHARMS checklist. PLoS Med 2014;11:e1001744. [Crossref] [PubMed]
- Bristol U of. QUADAS-2. Accessed October 4, 2023. Available online: https://www.bristol.ac.uk/population-health-sciences/projects/quadas/quadas-2/
- Stang A. Critical evaluation of the Newcastle-Ottawa scale for the assessment of the quality of nonrandomized studies in meta-analyses. Eur J Epidemiol 2010;25:603-5. [Crossref] [PubMed]
- Hanley JA, McNeil BJ. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983;148:839-43. [Crossref] [PubMed]
- Truong VT, Beyerbach D, Mazur W, et al. Machine learning method for predicting pacemaker implantation following transcatheter aortic valve replacement. Pacing Clin Electrophysiol 2021;44:334-40. [Crossref] [PubMed]
- Agasthi P, Ashraf H, Pujari SH, et al. Prediction of permanent pacemaker implantation after transcatheter aortic valve replacement: The role of machine learning. World J Cardiol 2023;15:95-105. [Crossref] [PubMed]
Cite this article as: Dell’Aquila M, Rossi CS, Caldonazo T, Rahouma M, Harik L, Cancelli G, Ibrahim M, Van den Eynde J, Soletti GJ, Leith J, Demetres M, Dimagli A, Gaudino M. Machine learning versus logistic regression for permanent pacemaker implantation prediction after transcatheter aortic valve replacement—a systematic review and meta-analysis. J Med Artif Intell 2024;7:32.



