
A predictive tool to forecast the Model for End-Stage Liver Disease score: the “MELDPredict” tool
Highlight box
Key findings
• When predicting Model for End-Stage Liver Disease (MELD) score in an auto-regressive setup, the state-of-the-art machine learning models performed significantly better than linear regression models.
• Extreme Gradient Boosting (XGBoost) and Random Forest Regression (RFR) models have the best prediction accuracy.
• Models’ performance generally deteriorates when the forecasting window increases and the amount of training data declines.
What was recommended and what is new?
• Performance of machine learning models worsen when the amount of training data declines.
• In the task of predicting MELD score in an autoregressive setup, XGBoost and RFR outperform long short-term memory—a state-of-the-art recurrent neural network model.
What is the implication, and what should change now?
• A quantitative tool to forecast MELD score for end-stage liver disease patients can help determine the best course of treatment based on the estimated progression of liver disease sickness.
• The resulting MELDPredict tool adds to clinical decision-making process and help to determine the next estimated MELD for patients.
Introduction
Liver transplantation (LT) is the ultimate hope for patients with end-stage liver disease with no alternative therapeutic approach. Every year, more patients are added to the waitlist, and many more need to be waitlisted. Although the number of LT procedures performed annually has increased by around 45% over the last 10 years (10,126 in 2023), many patients die waiting for an organ or are removed from the waitlist for being too sick to undergo LT (2,278 in 2023) (1,2), representing more than 20% of the waitlisted LT patients. The Model-for-End-Liver-Disease (MELD) score was implemented in 2002 and refined in 2016 with the addition of sodium (Na) to its original formula, and later in 2023, MELD 3.0 (3,4), with the addition of sex. The MELD adoption aims to decrease mortality on the waitlist by prioritizing the sickest patients for LT; i.e., MELD is proportional to the likelihood of a patient dying in 90 days unless undergoing LT. The MELD has been proven a good predictor of 90-day mortality without a transplant. With no alternative methods, MELD is currently used as the gold standard to prioritize patients for transplantation; thus, having a higher MELD score, would place patients in a higher place on the waitlist, and consequently, closer to LT. However, there is no quantitative method to forecast future MELD scores. With no quantitative method to forecast MELD progression, neither short- or long-term, while on the waitlist or in any other real-world clinical situation (e.g., whether to list a patient now or wait a couple more days); care teams and patients don’t have an objective way of better estimating how long patients still can wait until the LT. Such estimate could help directing whether that time can be used to better address pre-transplantation needs and patients be better clinically prepared for LT.
Currently, with no computational method to forecast future MELD, the estimate is made based on subjective clinical evaluation and on the clinical status of the patient at that moment of evaluation, relying largely on clinical experience and similar cases progression. Further, due to the high demand for resources around the transplant event, with an objective and more reliable tool, from a patient perspective, it can help better plan their own resources (family support, stay closer to the hospital, financial investment for the procedure, etc.). From a clinician perspective, an estimated MELD progression has the potential to provide a better understanding on how close patients are to the transplant event and use the remaining time to prioritize unmet needs (e.g., pre-transplant evaluations, addressing key determinants for transplant success); thus, being patients better clinically managed by the time LT happens. It is important to note that such a computational method would not replace clinical expertise, but not all clinicians have the same expertise and long-term experience, and due to the complexity of many of these cases, an objective tool can facilitate clinical decision-making when clinical presentations are uncertain; thus, a computational tool would add to the existing clinical knowledge for better and personalized decision-making.
This study addresses this gap, proposing a quantitative method “MELDPredict” to forecast MELD progression and what care teams and patients can expect regarding liver disease progression when in need of a LT (5-7). A computational method to estimate future (and at multiple times) MELD scores would support better clinical management based on the expected (and how much time) to the next score patients have, reinforce shared decision-making by empowering not only clinicians but also patients on their own care, and would provide a quantitative tool to support clinicians in determining the future course of care. While the MELD score is integral for prioritizing patients on the liver transplant waitlist, the availability of compatible liver grafts and their match with recipient characteristics are also vital factors influencing transplantation outcomes. However, while managing patients on the waitlist, is unknown when and whether grafts will become available, and neither is known the quality of such available grafts; thus, the importance of optimal and timely management of waitlisted patients.
To achieve this goal, we carry out experiments which test performance of different regression models in different scenarios commonly found in clinical practice, such as (I) comparing how models perform when clinicians want to increase the number of days for the future MELD score predictions based on a determined number of previous MELD score observations; and (II) comparing how models perform in predicting determined future MELD scores when clinicians have a more flexible number of previous MELD score observations. The experiments also aim to demonstrate improved performance of machine learning (ML) models compared to LR, a well-known baseline regression model.
With the aim of making this study results available for clinical practice with potential to speed implementation based on real-world prospective scenarios, resulting tool is translated into an automated and free online tool “MELDPredict” for everyone to test the prediction tool in real-world cases (8). The source code for the models is available in GitHub (9).
Methods
This is a retrospective study design using electronic health records (EHRs) from a Midwest institution through the University of Minnesota Clinical and Translational Science Institute (CTSI) (10) collected between 2006 and 2021. All data were managed and analyzed inside the Minnesota Supercomputing Institute and the CTSI secure environment. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the University of Minnesota Institutional Review Board (No. #00000092) and individual consent for this retrospective analysis was waived.
We carried out four experiments, matching different clinical needs. In experiment 1, we observe MELD of the past 5 days (h=5) and predict next day MELD (f=1). This addresses the urgent scenario where clinicians need to know patient’ next day MELD. In experiment 2, we observe MELD of the past 5 days (h=5) and predict the next 7 days MELD (f=7). This addresses the scenario where clinicians need to know the trajectory of patient MELD in the near future, but not that close to the current day, and even whether patients could wait a little longer for an organ. Since there is no pre-determined requirement for h and f clinically, we selected h manually based on typical data availability, with the goal of optimizing model performance. We also experimented on (h=5, f=3) and (h=5, f=5) to study how the models’ performance changes when predicting longer windows. Figure 1 represents the overall study design. It is important to note that while our study evaluates MELD scores calculated frequently (every 2 to 5 days), this practice is generally reserved for patients with higher MELD scores due to or liver disease progression or due to other clinical deteriorations needing hospitalization (e.g., infection, ascites), as frequent calculations do not consistently translate into improved outcomes for all patients, but it’s a reflection of patients health status.
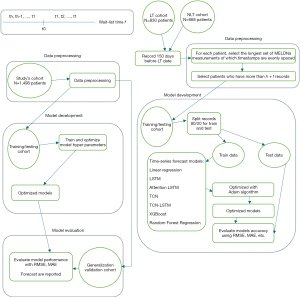
Cohort selection and data description
All patients 18 years or older who were waitlisted for LT between 2006 and 2021 were included. This selection captured both patients who underwent LT (n=830) and those who were still waiting or were removed [non-LT (NLT), n=668] from the waitlist, totaling 1,498 initial waitlisted patients. The features for the analytical data set included patient’s MELDNa scores (MELD with Na which was in use at the time of the conception of this study) and their timestamp while on the waitlist. MELDNa score was calculated based on laboratory values at any point when the features [creatinine, Na, bilirubin, and international normalized ratio (INR)] were available according to national policies (11). Missing values for bilirubin and INR were imputed using the last observation carried forward method (12). Values for missing creatinine and Na were not imputed due to their high (and often) variability and those missing observations were excluded. The formula for MELDNa scores calculation is shown below. For this study, MELDNa score is considered as the native MELD, with no exception points added.
Data preprocessing and validation
For each patient, we select the MELDNa scores from consecutive days, such that the length of the sequence of scores are greater than or equal to (h + f). For score sequences that are less than (h + f), we interpolate and select sequences with at most 10% data missing. However, to ensure integrity of model testing, the test data neither f sequences do not contain interpolated data points. After preprocessing all records, we selected 80% of patients, who were ranked by the amount of available data, with the aim of harvesting as much data to train the models as possible in both the train and test steps of the models (hereby will be referred to as the train/test cohort). For each patient in the train/test cohort, we use patients’ last MELDNa score sequences (timewise) to test the models, and the previous ones to train the models. We then validate the model generalization capability by measuring their performance on the remaining 20% of patients (hereby will be referred to as the generalize cohort).
Statistical analysis
We use descriptive to describe the included cohorts. Continuous features are described as mean and standard deviation (SD), and categorical data as counts and percents (%). Demographics data is used just to describe the included population, and MELDNa with its associated timestamp are used for modeling. We experimented with linear regression (LR) model and two classes of ML models: recurrent neural network (RNN) and ensemble learning (EL). All models are experimented within an autoregressive setup. We performed four experiments, with (h=5, f=1), (h=5, f=3), (h=5, f=5) and (h=5, f=7). Figures S1,S2 in Appendix 1 provide a visual representation of this setup. The clinical purpose of this setup is explained previously. It is worth noting that when f increases, the number of sequences that can be used to train the models (hereby denoted xa) decreases. We will discuss this decrease and its impact on the models’ performance more in the “Results” and “Discussion” sections.
LR
We apply the LR model to the pre-processed data (that we previously mentioned in the “Data preprocessing and validation” section). The result of this setup is used as a baseline model for the ML models’ performance. We also study performance of the LR model in an independent configuration, i.e., in which the independent variable is the timestamp of MELD score measurement and the dependent variable is the MELD score. That setup is less comparable with the rest of the ML models; thus, we report details of the setup as well as how the LR model performed in Tables S1-S4 in Appendix 2.
RNN
RNN is a class of ML models designed to handle sequential data. Unlike traditional neural networks, RNNs have connections that form directed cycles, allowing information to persist and influence subsequent steps in the sequence. This makes them particularly effective for tasks such as natural language processing, speech recognition, and time-series prediction, where context and order of data points are crucial. We experimented with four RNN models: long short-term memory (LSTM), attention LSTM (A-L), temporal convolutional network (TCN), and TCN LSTM (T-L). Among those models, LSTM is a state-of-the-art model in the task of time series prediction, while TCN and T-L are more recent models.
LSTM and A-L
LSTM is a state-of-the-art time-series forecasting (TSF) model (13), which has shown to outperform previous RNN architectures (14,15). To implement LSTM, we utilized Pytorch’ LSTM library. The optimized hyper parameters of the LSTM model are reported in Table S5 in Appendix 3.
Attention is a ML mechanism which dynamically focuses on the most relevant parts of the input data, therefore potentially better selects input or decoded sequence and improves the model’ information processing capability (16). Recently, it has been widely used and is gaining popularity in the task of time series prediction. Most introduced models combine an attention layer with a LSTM layer (17-19). In this paper, we constructed the A-L model in a similar fashion: it consists of a MultiHeadAttention layer (20) and an LSTM encoder-decoder layer. The optimized hyper parameters of the A-L model are reported in Table S6 in Appendix 3.
TCN and T-L
TCNs (21) are a class of neural network models designed for sequential data, offering an alternative to RNNs. TCNs use multiple convolutional neural network (CNN) layers with causal padding to ensure that the predictions at a given time step depend only on past inputs, thereby maintaining the sequence order. They are known for their ability to capture long-term dependencies more effectively than traditional RNNs and have been shown to outperform LSTMs in weather forecasting (22), a prominent application of TSF. We also experimented with a combined T-L model, similar to those in (23), containing both a TCN layer and a LSTM layer, to evaluate whether stacking these two models can improve performance. We report the optimized hyper-parameters for the TCN and T-L model in Tables S7,S8 in Appendix 3.
EL
EL involves combining multiple ML models to improve overall performance. Ensemble methods are widely used in practice due to their ability to reduce overfitting and increase model stability. Two of the most common techniques in EL are bagging and boosting. Bagging, such as in random forests, involves training multiple models on different subsets of the data and averaging their predictions. Boosting, exemplified by algorithms like Gradient Boosting, sequentially trains models to correct errors made by previous models. In this paper, we evaluate three such models: Extreme Gradient Boosting (XGBoost) (24), Random Forest Regression (RFR) (25), and Extra Tree Regressor (EVR) (26). All of these models have been applied to TSF for a wide variety of targets, ranging from predicting rainfall (27) to apartment prices (28), achieving state-of-the-art performance. We used the sklearn ExtraTreeRegressor (29) and RandomForestRegressor (30) library for RFR and EVR; and the Xgboost repository on GitHub (31) for XGBoost. The optimized hyper parameters of the RFR, EVR, and XGBoost models are reported in Tables S9-S11 in Appendix 3.
Model optimization and hyper-parameter tuning
All models were optimized using standard techniques: the LSTM, A-L, TCN, and T-L models were optimized using the Adam Optimizer algorithm (32), and hyper-parameter tuning was carried out using the Optuna framework (33). Sklearn library implements the optimizers for the RFR, EVR, and XGBoost models and hyper-parameters were tuned using the HalvingGridSearchCV package of Sklearn (34) (using factor =10, cv =2). Tables S12,S13 in Appendix 4 provide all packages and versions used for the analysis in this study.
Model performance evaluation
The train/test is performed with 80% of the sample, and 20% is used for generalization. Our evaluation is done on two data sets. First, we evaluate the performance of models on the train/test data set through 5-fold validations. We also evaluate the generalization capability of the models by measuring their performance on the generalize data set (the construction of which is previously mentioned). We evaluated the accuracy of models’ prediction and the quality of the model using R-square, mean absolute error (MAE) and root mean square error (RMSE) of its forecast on the whole cohort. For f>1, we also report 95% confidence interval (CI) of the models’ predictions, as well as the RMSE of each predicting timestep.
To compare the forecasting capability of the models, we performed the Diebold-Mariano (DM) test. The classical DM test was originally proposed by Diebold and Mariano (35). It then became a popular test to compare the predictive accuracy of two competing forecast models. It evaluates whether there is a significant difference in the forecast errors of the models, providing a robust measure for model performance comparison. We selected XGBoost as the base model for comparison against all other models, given that it generally has the best accuracy (as will be described more in the “Results” section). The null hypothesis is that there is no statistically significant difference in the two models’ forecast accuracy. We reject the null hypothesis if P is less than the selected alpha 0.05. This choice of significance level is a conventional threshold commonly used in hypothesis testing. If the performances of two models are statistically significantly different, we rely on RMSE and MAE to judge which model is better.
Results
A total of 1,498 patients were included. The description of both LT and NLT are very similar and do not show significant variations. The results show that included cohorts for LT and NLT are similar to the national population regarding demographics and MELDNa characteristics; thus, being a good picture of the waitlisted patients in the United States. The mean age was 54.58 (SD =10.89) years for the LT cohort, and 53.61 (SD =10.16) years for the NLT cohort. The majority was male with 68.80% and 60.33% in the LT and NLT cohorts, respectively. Regarding race, the majority was White/Caucasian, with 82.10% and 83.95% across LT and NLT, respectively. The mean MELDNa for the LT cohort was 23.95 (SD =9.87), and for the NLT cohort 24.56 (SD =9.82).
Figure S3 in Appendix 5 displays the daily mean and SD of the data used specifically for the analysis. It is worth noting that even though the line of average MELDNa is mostly flat, the SD for each day (time step) is large, indicating high variation of MELD in the cohort.
State-of-the-art ML models achieve much better accuracy than LR
All state-of-the-art ML models have better prediction accuracy than the LR model in all experiments. In the test data set, LR best RMSE =4.621, when f=1, compared to the RMSE =2.582 of the best performance ML model, the RFR. In the generalize data set, LR achieved the best RMSE =4.137, when f=1, compared to the RMSE =2.883 of the best performance ML model, the RFR. This difference is even more noticeable when predicting longer time windows. For instance, the best performed state-of-the-art ML model, the XGBoost model, achieves RMSE =3.113 on test data set for f=3, a 62.5% improvement over RMSE =9.595 achieved by LR. Even the worst state-of-the-art model experimented, the LSTM model, outperforms LR. In the (h=5, f=1) setup, where LR has the best performance (out of all experiments), LSTM achieves 36.45% improvement over LR model prediction accuracy on test data set and 19.33% on generalize data set. Table 1 describes the improvement in accuracy—reflected by RMSE—between the ML models and the LR model in all experiments. As previously mentioned, we also evaluated the prediction accuracy of the models with MAE, for which we observed the same result (Appendix 6). We report the RMSE and MAE of all models in all experiments in Tables S1-S4 in Appendix 2.
Table 1
| Models | Test data set | Generalize data set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| f=1 | f=3 | f=5 | f=7 | f=1 | f=3 | f=5 | f=7 | ||
| RFR (%) | 44.12 | 45.07 | 37.69 | 58.43 | 30.31 | 48.56 | 40.23 | 64.95 | |
| EVR (%) | 40.71 | 41.49 | 33.34 | 57.36 | 28.40 | 45.38 | 36.05 | 62.04 | |
| XGBoost (%) | 44.25 | 45.11 | 37.79 | 58.77 | 29.76 | 48.75 | 36.45 | 64.23 | |
| LSTM (%) | 36.46 | 31.12 | 17.65 | 50.89 | 19.34 | 35.87 | 20.29 | 55.29 | |
It is measured by the formula: [(RMSE of LR model) – (RMSE of ML model)]/(RMSE of LR model) × 100%. RMSE, root mean square error; ML, machine learning; LR, linear regression; h, historical data; f, future forecasts; RFR, Random Forest Regression; EVR, Extra Tree Regressor; XGBoost, Extreme Gradient Boosting; LSTM, long short-term memory.
XGBoost and RFR have the best accuracy among all models
As previously mentioned, we compare the XGBoost models against other models using the DM test. The accuracy of XGBoost is not statistically different to RFR—we observed P>0.05 in all experiments. The P values are documented in Tables 2,3. Performance of RFR and XGBoost is significantly different from the rest of the models in all experiments—as proven by the P, as also documented in Tables 2,3. Combining this with the fact that XGBoost and RFR have lowest RMSE/MAE among all models in all experiments (Tables S1-S4 in Appendix 2), our results show that XGBoost and RFR has best forecasting accuracy than the rest of the models (including LSTM and others). As shown in our results, XGBoost and RFR achieved significantly different performance when compared to LSTM, indicating their superior predictive capabilities in this context. The only worth-mentioning exception is in (h=5, f=3) experiment where A-L has the best RMSE in the generalize data set. It achieved RMSE = 2.699, compared to RMSE =2.739 for XGBoost model (Table S2 in Appendix 2). However, as noticed in Tables 2,3, the difference is not statistically significant (P=0.20 and P=0.29 in test and generalize cohort, respectively).
Table 2
| f | RFR | EVR | LSTM | A-L | TCN | T-L | LR |
|---|---|---|---|---|---|---|---|
| 1 | 0.81* | 0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| 3 | 0.84* | 0.007 | <0.001 | 0.20* | <0.001 | <0.001 | <0.001 |
| 5 | 0.93* | 0.003 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| 7 | 0.46* | 0.11* | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
*, P value >0.05. XGBoost, Extreme Gradient Boosting; f, future forecasts; RFR, Random Forest Regression; EVR, Extra Tree Regressor; LSTM, long short-term memory; A-L, attention LSTM; TCN, temporal convolutional network; T-L, TCN LSTM; LR, linear regression.
Table 3
| f | RFR | EVR | LSTM | A-L | TCN | T-L | LR |
|---|---|---|---|---|---|---|---|
| 1 | 0.56* | 0.49* | 0.01 | <0.001 | <0.001 | <0.001 | <0.001 |
| 3 | 0.90* | 0.18* | 0.002 | 0.29* | <0.001 | <0.001 | <0.001 |
| 5 | 0.003 | 0.90* | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| 7 | 0.40* | 0.11* | 0.01 | <0.001 | <0.001 | <0.001 | <0.001 |
*, P value >0.05. XGBoost, Extreme Gradient Boosting; f, future forecasts; RFR, Random Forest Regression; EVR, Extra Tree Regressor; LSTM, long short-term memory; A-L, attention LSTM; TCN, temporal convolutional network; T-L, TCN LSTM; LR, linear regression.
Increasing predicting window generally decreases model performance
For most models, when the predicting window f increases, we observed a slight deterioration in the accuracy of the model prediction. This is reflected by the decrease of the models R-square and the increase of error of the models’ prediction. For instance, R-square of the best-performed ML model, the XGBoost model, falls from 0.90 to 0.84, 0.78, and 0.71 when f increases from 1 to 3, to 5 to 7, respectively. Interestingly, that is not the case for all ML models. Tables 4,5 describe the changes in models RMSE when f increases from 1 to 7. The R-square of all models are reported in Tables S1-S4 in Appendix 2.
Table 4
| f | RFR (%) | EVR (%) | XGBoost (%) | LSTM (%) | A-L (%) | TCN (%) | T-L (%) | LR (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | +0 | +0 | +0 | +0 | +0 | +0 | +0 | +0 |
| 3 | +20.64 | +21.09 | +20.85 | +33.04 | −63.37 | −11.77 | −39.72 | +22.72 |
| 5 | +39.19 | +40.33 | +39.29 | +61.78 | −0.67 | −9.09 | −7.37 | +24.82 |
| 7 | +54.49 | +49.31 | +53.57 | +60.49 | −9.03 | −5.22 | −43.97 | +107.64 |
The baseline is the (h=5, f=1) setup. The accuracy is measured on the train/test cohort. RMSE, root mean square error; f, future forecasts; RFR, Random Forest Regression; EVR, Extra Tree Regressor; LSTM, long short-term memory; A-L, attention LSTM; TCN, temporal convolutional network; T-L, TCN LSTM; LR, linear regression; h, historical data.
Table 5
| f | RFR (%) | EVR (%) | XGBoost (%) | LSTM (%) | A-L (%) | TCN (%) | T-L (%) | LR (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | +0 | +0 | +0 | +0 | +0 | +0 | +0 | +0 |
| 3 | −4.65 | −1.45 | −5.75 | +2.70 | −69.86 | −11.25 | −41.17 | +29.18 |
| 5 | +6.97 | +11.41 | +12.84 | +23.25 | −4.68 | −15.66 | −7.90 | +24.73 |
| 7 | +13.91 | +20.09 | +15.35 | +25.53 | −2.04 | −0.54 | −31.25 | +126.49 |
The baseline is the (h=5, f=1) setup. The accuracy is measured on the generalize cohort. RMSE, root mean square error; f, future forecasts; RFR, Random Forest Regression; EVR, Extra Tree Regressor; LSTM, long short-term memory; A-L, attention LSTM; TCN, temporal convolutional network; T-L, TCN LSTM; LR, linear regression; h, historical data.
Discussion
This study aimed to develop and validate a method to forecast with high accuracy future MELDNa scores based on patients’ observed scores. To our knowledge, this is the first quantitative method that achieved that goal, and with success. We applied a wide range of regression models, including traditional statistical models (LR), state-of-the-art ML models (RFR, EVR, XGBoost, and LSTM), and more recently introduced ML models (TCN and T-L). The fact that all state-of-the-art ML models outperform LR validates the high capability of such models in detecting non-linear relationships in the data, in this case MELDNa measurements, which LR encounters challenges in.
The decrease in performance of the models, which generally deteriorates as f increases, can be explained by the significant decrease in the amount of train data. As an illustration, Table 6 outlines characteristics of the train data when the length of the predicting window changes. Since a lot of patients don’t have consistent measurements on consecutive days, a requirement to apply the time series models, when increasing the length of the predicting window, there is less data to train the models on. When increasing f from 1 to 7, the total number of patients of whom data can be used reduces from 591 to 230 patients (a 61.017% reduction). The number of sequences that the models can train on (xa, as referred to in Figure 1) falls from 8,549 to 2,769 (a 67.61% reduction). Since the quality of ML models, especially neural networks, generally correlates with the amount of data that they can train on, it is to be expected that the performance might falter. However, as previously mentioned, the observed decline isn’t significant. Our results show that XGBoost and RFR models prove to be able to predict future MELDNa scores for patients up to 7 days with high accuracy.
Table 6
| Experiment | Total number of patients (including train, test, and external validation) | xa |
|---|---|---|
| Exp 1 (h=5, f=1) | 591 | 8,549 |
| Exp 2 (h=5, f=3) | 436 | 5,448 |
| Exp 3 (h=5, f=5) | 306 | 3,521 |
| Exp 4 (h=5, f=7) | 230 | 2,769 |
xa is the number of training sequences, previously mentioned in Figure 1. Exp, experiment; h, historical data; f, future forecasts.
Our results provide valuable knowledge to the current understanding of MELDNa progression and its forecasting. Clinically, understanding the capability of predicting waitlisted patients’ future MELDNa score adds to the current evidence and provides a quantitative way of evaluating MELDNa progression at the point of care. To our knowledge, this has not been demonstrated before and represents a critical need for the liver transplant community (5,36,37). In addition to aiding clinical evidence, it has the potential to empower patients and engage them (along with clinicians) in the decision-making process regarding their own disease progression and what can be expected in the future, specifically in the short term, when disease progresses fast, and decisions need to be made and revisited day-by-day. This information is essential not just useful for forecasting closeness to the LT, but also when clinicians and patients need to decide what are the next steps regarding placement on the waitlist, answering the so far unanswered clinical question: “Can the patient wait one more day or need to be placed on the waitlist now?”. This specific case happens when patients are under evaluation to be placed on the waitlist, but they are very sick, and clinicians are uncertain if patients can finalize pre-waitlist evaluations before undergoing a LT. It also provides a better understanding of how far from the transplant date patients are based on the predicted future MELDNa score (i.e., higher MELDNa places patients higher on the waitlist).
This quantitative way of predicting future MELDNa scores can further serve as an adjunct tool to answer so far unknown clinicians and patients’ questions, such as “How much time do patients need to wait until they are closer to receive an organ?”, “Will patients MELDNa progress slower or faster?”, “Do patients need to plan to be closer to the hospital soon?”, “Does clinical team still have time to intervene on patients before LT?”. Successful implementation of such a quantitative tool has also the potential to empower patients to better engage in their health management during the period before transplant and increase not just transplant success but also overall patient satisfaction, as they can be more active participants on shared-decision making (37-39).
Results of this study also show that state-of-the-art ML models (LSTM, XGBoost, RFR, and EVR) are good candidates to predict the future MELDNa score of a patient or a cohort. This may be due to the nature of the dataset used in this study, which is characterized by high dimensionality and sparsity, making it particularly well-suited for the strengths of XGBoost (24) and RFR. These models are specifically designed to manage such complexities, which is likely a contributing factor to their enhanced performance relative to LSTM. While LSTM models excel in sequential data applications (13), excel in sequential data applications, their performance may diminish in scenarios involving high noise and less clear temporal dependencies, as observed in our study. This further reinforces the suitability of tree-based models like XGBoost and RFR for the given dataset. Further, the ability of XGBoost and RFR to effectively capture non-linear relationships and interactions among features not only underscores their robustness in this study but also highlights their potential utility in clinical decision-making (40), where data is often intricate and multifaceted. They can predict with good accuracy the next day’s MELD score (best RMSE =2.582) and near future MELD scores up to 7 days (best RMSE =3.284). Given a patient for whom h MELDNa data points have been observed and f MELDNa data points need to be predicted, clinicians could follow steps as demonstrated in our study design.
Further, based on this study, we develop “MELDPredict”, a user-friendly tool, and make “MELDPredict” freely available to the entire community to use as adjunct tool to estimate MELDNa progression to inform clinical decision-making. While our MELDPredict tool provides valuable insights into future MELD score predictions for waitlisted patients, it is essential to recognize that successful LT outcomes depend on various factors, including the availability of compatible and of high-quality grafts. Further improvements will be made in the near future with the addition of sex, in order to be able to capture MELD 3.0. Different from other MELDNa features, sex is static (does not change day-by-day), thus we expect sex to have minimal impact on the performance and capabilities of the tool forecasting MELD.
This study has many strengths, such as the granularity of the data derived from real-world EHRs, models are trained and validated on different cohorts, and comparison among a vast range of ML models. Most importantly, the work provides a ready to use tool “MELDPredict” for clinicians to augment their decision-making in a daily basis in real-world scenarios. Considering this study was conceptually developed while MELD 3.0 was not yet adopted, additional steps are the adjustments of the proposed model with MELD 3.0 information, and the inclusion of sex as part of the “MELDPredict” tool. While our study successfully demonstrates the ability of ML models, particularly XGBoost and RFR, to accurately predict future MELD scores, we acknowledge that predicting clinical outcomes is equally crucial. Integrating comprehensive clinical data, including patient background, primary disease, comorbidities, and interventions, could significantly enhance the predictive power of our models and provide a more holistic view of patient trajectories. Future research will explore the incorporation of these clinical variables into MELDPredict to improve its applicability in clinical decision-making.
Conclusions
In this study, we demonstrated the notable performance of XGBoost and RFR in solving a critical clinical question: to provide a computational method to predict future MELDNa score for patients with end-stage liver disease, compared to other well-established ML models (such as LSTM, TCN, etc.), and traditional statistic model, such as LR. To our best knowledge, this study is the first ML approach to predict future MELDNa of patients waiting for LT, and to deliver a ready to use tool “MELDPredict”. Specifically, it is the first quantitative method to predict future MELDNa that goes beyond a subjective method based mostly on content knowledge (e.g., clinical knowledge and experience). Further, clinicians have the potential to incorporate into their practice a quantitative metric and share it with patients in a more user-friendly way for health decision-making. This information is essential when clinicians and patients decide what are the next steps regarding placement on the waitlist, time to complete pre-transplant evaluations to increase transplantation success, and how far from the LT patients are, based on the predicted future MELDNa score. This quantitative way of predicting future MELDNa score can serve as an adjunct tool to answer so far unknown clinicians and patients’ questions of MELDNa next score and guide future course of care. A better estimate of MELDNa progression would greatly reinforce shared decision-making; thus, empowering not just clinicians but patients on their own care.
Acknowledgments
Preliminary findings of this work were presented as a poster entitled “Artificial Neural Network Application for MELDNa Prediction” at the 2021 American Transplant Congress (https://atcmeetingabstracts.com/abstract/artificial-neural-network-application-for-meldna-prediction/).
Footnote
Data Sharing Statement: Available at https://jmai.amegroups.com/article/view/10.21037/jmai-24-277/dss
Peer Review File: Available at https://jmai.amegroups.com/article/view/10.21037/jmai-24-277/prf
Funding: This work was partially supported by
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jmai.amegroups.com/article/view/10.21037/jmai-24-277/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the University of Minnesota Institutional Review Board (No. #00000092) and individual consent for this retrospective analysis was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- National Data - OPTN. [Cited 2019 Apr 14]. Available online: https://optn.transplant.hrsa.gov/data/view-data-reports/national-data/
- Benckert C, Quante M, Thelen A, et al. Impact of the MELD allocation after its implementation in liver transplantation. Scand J Gastroenterol 2011;46:941-8. [Crossref] [PubMed]
- Kamath PS, Wiesner RH, Malinchoc M, et al. A model to predict survival in patients with end-stage liver disease. Hepatology 2001;33:464-70. [Crossref] [PubMed]
- Goudsmit BFJ, Putter H, Tushuizen ME, et al. Validation of the Model for End-stage Liver Disease sodium (MELD-Na) score in the Eurotransplant region. Am J Transplant 2021;21:229-40. [Crossref] [PubMed]
- Vagefi PA, Bertsimas D, Hirose R, et al. The rise and fall of the model for end-stage liver disease score and the need for an optimized machine learning approach for liver allocation. Curr Opin Organ Transplant 2020;25:122-5. [Crossref] [PubMed]
- Merion RM, Wolfe RA, Dykstra DM, et al. Longitudinal assessment of mortality risk among candidates for liver transplantation. Liver Transpl 2003;9:12-8. [Crossref] [PubMed]
- Chandraker A, Andreoni KA, Gaston RS, et al. Time for reform in transplant program-specific reporting: AST/ASTS transplant metrics taskforce. Am J Transplant 2019;19:1888-95. [Crossref] [PubMed]
- Pruinelli L, Nguyen M. MELDPredict Tool. 2024. [Cited 2024 Nov 25]. Available online: https://ml-meld-prediction.onrender.com/
- Nguyen M. MELDPredict GitHub Source. 2024. [Cited 2024 Nov 25]. Available online: https://github.com/minhng22/meld-prediction-umn
- Clinical and Translational Science Institute - University of Minnesota. Clinical Data Repository. [Cited 2022 Jul 5]. Available online: https://ctsi.umn.edu/services/data-informatics/clinical-data-repository
- Unos. MELD and PELD Calculators User Guide. Available online: https://optn.transplant.hrsa.gov/media/qmsdjqst/meld-peld-calculator-user-guide.pdf
- Salkind NJ. Last Observation Carried Forward. In: Salkind NJ. editor. Encyclopedia of Research Design. Thousand Oaks: SAGE Publications, Inc.; 2010.
- Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput 1997;9:1735-80. [Crossref] [PubMed]
- Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans Neural Netw 1994;5:157-66. [Crossref] [PubMed]
- Srivastava N, Mansimov E, Salakhudinov R. Unsupervised learning of video representations using lstms. In: Proceedings of the 32nd International Conference on Machine Learning. PMLR; 2015:843-52.
- Luong T, Pham H, Manning CD. Effective Approaches to Attention-based Neural Machine Translation. In: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing. 2015:1412-21.
- Liang Y, Ke S, Zhang J, et al. GeoMAN: Multi-level Attention Networks for Geo-sensory Time Series Prediction. In: Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI-18). 2018:3428-34.
- Qin Y, Song D, Chen H, et al. A dual-stage attention-based recurrent neural network for time series prediction. In: Proceedings of the 26th International Joint Conference on Artificial Intelligence. 2017:2627-33.
- Zhang X, Liang X, Zhiyuli A, et al. At-lstm: An attention-based lstm model for financial time series prediction. IOP Conf Ser Mater Sci Eng 2019;569:052037.
- Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. In: NIPS'17: Proceedings of the 31st International Conference on Neural Information Processing Systems. 2017:6000-10.
- Bai S, Kolter JZ, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv:1803.01271 [Preprint]. 2018. Available online: https://arxiv.org/abs/1803.01271
- Hewage P, Behera A, Trovati M, et al. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput 2020;24:16453-82. [Crossref]
- Bi J, Zhang X, Yuan H, et al. A hybrid prediction method for realistic network traffic with temporal convolutional network and LSTM. IEEE Trans Autom Sci Eng 2021;19:1869-79. [Crossref]
- Chen T, Guestrin C. Xgboost: A scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2016:785-94.
- Breiman L. Random forests. Mach Learn 2001;45:5-32. [Crossref]
- Geurts P, Ernst D, Wehenkel L. Extremely randomized trees. Mach Learn 2006;63:3-42. [Crossref]
- Barrera-Animas AY, Oyedele LO, Bilal M, et al. Rainfall prediction: A comparative analysis of modern machine learning algorithms for time-series forecasting. Mach Learn Appl 2022;7:100204. [Crossref]
- Čeh M, Kilibarda M, Lisec A, et al. Estimating the performance of random forest versus multiple regression for predicting prices of the apartments. ISPRS Int J Geoinf 2018;7:168. [Crossref]
- ExtraTreesRegressor. scikit learn 1.5.2 documentation. [Cited 2024 Nov 25]. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.ExtraTreesRegressor.html
- RandomForestRegressor. scikit learn 1.5.2 documentation. [Cited 2024 Nov 25]. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html
- GitHub. dmlc/xgboost. [Cited 2024 Nov 25]. Available online: https://github.com/dmlc/xgboost/tree/master
- Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. In: Proceedings of the International Conference on Learning Representations (ICLR 2015). 2015.
- Akiba T, Sano S, Yanase T, et al. Optuna: A next-generation hyperparameter optimization framework. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2019:2623-31.
- HalvingGridSearchCV. scikit learn 1.5.2 documentation. [Cited 2024 Nov 25]. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.HalvingGridSearchCV.html
- Diebold FX, Mariano RS. Comparing predictive accuracy. Journal of Business & Economic Statistics 2002;20:134-44. [Crossref]
- Yao FY, Bass NM, Nikolai B, et al. A follow-up analysis of the pattern and predictors of dropout from the waiting list for liver transplantation in patients with hepatocellular carcinoma: implications for the current organ allocation policy. Liver Transpl 2003;9:684-92. [Crossref] [PubMed]
- Schold JD, Buccini LD, Phelan MP, et al. Building an Ideal Quality Metric for ESRD Health Care Delivery. Clin J Am Soc Nephrol 2017;12:1351-6. [Crossref] [PubMed]
- Husain SA, Brennan C, Michelson A, et al. Patients prioritize waitlist over posttransplant outcomes when evaluating kidney transplant centers. Am J Transplant 2018;18:2781-90. [Crossref] [PubMed]
- Lomotan EA, Meadows G, Michaels M, et al. To Share is Human! Advancing Evidence into Practice through a National Repository of Interoperable Clinical Decision Support. Appl Clin Inform 2020;11:112-21. [Crossref] [PubMed]
- Balakrishnan K, Olson S, Simon G, et al. Machine learning for post-liver transplant survival: Bridging the gap for long-term outcomes through temporal variation features. Comput Methods Programs Biomed 2024;257:108442. [Crossref] [PubMed]
Cite this article as: Nguyen M, Zhou J, Ma S, Simon G, Olson S, Pruett T, Pruinelli L. A predictive tool to forecast the Model for End-Stage Liver Disease score: the “MELDPredict” tool. J Med Artif Intell 2025;8:45.


